User Guide
Package ‘photobiologyPlants’ 0.6.1.1.9003
Pedro J. Aphalo
2026-07-25
Source:vignettes/user-guide.Rmd
user-guide.RmdIntroduction
This package provides data sets and functions relevant to the photobiology of plants. It is part of a suite, which has package ‘photobiology’ at its core. Please visit (http://www.r4photobiology.info/) for more details. For more details on plotting spectra, please consult the documentation for package ‘ggspectra’, and for information on the calculation of summaries and maths operations between spectra, please, consult the documentation for package ‘photobiology’.
See the User Guide for packages ‘photobiology’ and ‘ggspectra’ for instructions on how to work with spectral data. As package ‘ggspectra’ is only suggested, in this vignette it is loaded an used conditionally on its availability.
library(photobiology)
library(photobiologyPlants)
library(photobiologyWavebands)
eval_plots <- requireNamespace("ggspectra", quietly = TRUE)
if (eval_plots) library(ggspectra)
theme_set(theme_bw())Light environment
Photon ratios
R_FR() and other functions for computing photon ratios
are convenience functions implemented using function
q_ratio() and q_irrad() from package
‘photobiology’ and waveband definitions from package
‘photobiologyWavebands’ with defaults arguments to parameter
std for wavelength ranges commonly used in the field of
plant photobiology. These functions can be used with one or
more spectra as argument.
R_FR(sun.spct)## R:FR[q:q]
## 1.242474
## attr(,"radiation.unit")
## [1] "q:q ratio"Here, the argument named attr2tb is forwarded to method
q_ratio from package ‘photobiology’ to copy metadata from
the spectra into the returned data frame.
R_FR(sun_evening.spct,
std = "Smith20",
attr2tb = c("when.measured" = "time.UTC", "lat" = "latitude"))## # A tibble: 5 × 4
## spct.idx `R:FR[q:q]` time.UTC latitude
## <fct> <dbl> <dttm> <dbl>
## 1 time.01 1.18 2023-06-12 18:38:00 60.2
## 2 time.02 1.19 2023-06-12 18:39:00 60.2
## 3 time.03 1.18 2023-06-12 18:40:00 60.2
## 4 time.04 1.16 2023-06-12 18:41:00 60.2
## 5 time.05 1.12 2023-06-12 18:42:00 60.2Photoreceptors
Phytochromes: photoequilibrium
In the examples below we use the solar spectral data included in
package ‘photobiology’ in object sun.spct of class
source_spct.
We can calculate the phytochrome photoequilibrium from spectral irradiance data as follows.
Pfr_Ptot(sun.spct)## [1] 0.68341## # A tibble: 5 × 4
## spct.idx Pfr_Ptot time.UTC latitude
## <fct> <dbl> <dttm> <dbl>
## 1 time.01 0.671 2023-06-12 18:38:00 60.2
## 2 time.02 0.672 2023-06-12 18:39:00 60.2
## 3 time.03 0.670 2023-06-12 18:40:00 60.2
## 4 time.04 0.669 2023-06-12 18:41:00 60.2
## 5 time.05 0.664 2023-06-12 18:42:00 60.2We can also calcualte the red:far-red photon ratio, in this third example, for the same spectrum as in the first example
R_FR(sun.spct)## R:FR[q:q]
## 1.242474
## attr(,"radiation.unit")
## [1] "q:q ratio"which is equivalent to calculating it using package ‘photobiology’ directly
## R:FR[q:q]
## 1.266704
## attr(,"radiation.unit")
## [1] "q:q ratio"We can, and should whenever spectral data are available, calculate the photoequilibrium as above, directly from these data. It is possible to obtain and approximation in case of the solar spectrum and other broad spectra, using the red:far-red photon ratio. The calculation, however, is only strictly valid, for di-chromatic illumination with red plus far-red light.
Pfr_Ptot_R_FR(R_FR(sun.spct))## R:FR[q:q]
## 0.7025925
Pfr_Ptot_R_FR(R_FR(sun.spct, std = "Smith10"))## R:FR[q:q]
## 0.7051691Here we calculated the R:FR ratio from spectral data, but in practice one would use this function only when spectral data is not available such as when a R plus FR sensor is used. We can see that in such a case the photoequilibrium calculated is only a rough approximation. For sunlight, in the example above when using spectral data we obtained a value of 0.683 in contrast to 0.703 when using the R:FR photon ratio. For other light sources differences can be much larger. Furthermore, here we used the true R:FR ratio calculated from the spectrum, while broad-band red:far-red sensors give only an approximation, which is good for sunlight, but which will be inaccurate for artificial light, unless a special calibration is done for each type of lamp. There are differences in the wavelength sensitivity between sensors from different suppliers and even between models from a given supplier. In addition, as the definition of the R:FR photon ratio used as the basis for calibration by different suppliers is not the same, the R:FR reported by difference sensors varies even under sunlight.
In the case of monochromatic light we can still use the same functions, as the defaults are such that we can use a single value as the ‘w.length’ argument, to obtain the Pfr:P ratio. For monochromatic light, irradiance is irrelevant for the photoequilibrium (steady-state).
Pfr_Ptot(660)## [1] 0.869649
Pfr_Ptot(735)## [1] 0.01749967## [1] 0.86964902 0.01749967
Pfr_Ptot(435)## [1] 0.3859998We can also plot Pfr:Ptot as a function of wavelength (nm) of
monochromatic light. The default is to return a vector for short input
vectors, and a response_spct object otherwise, but this can
be changed through argument spct.out.
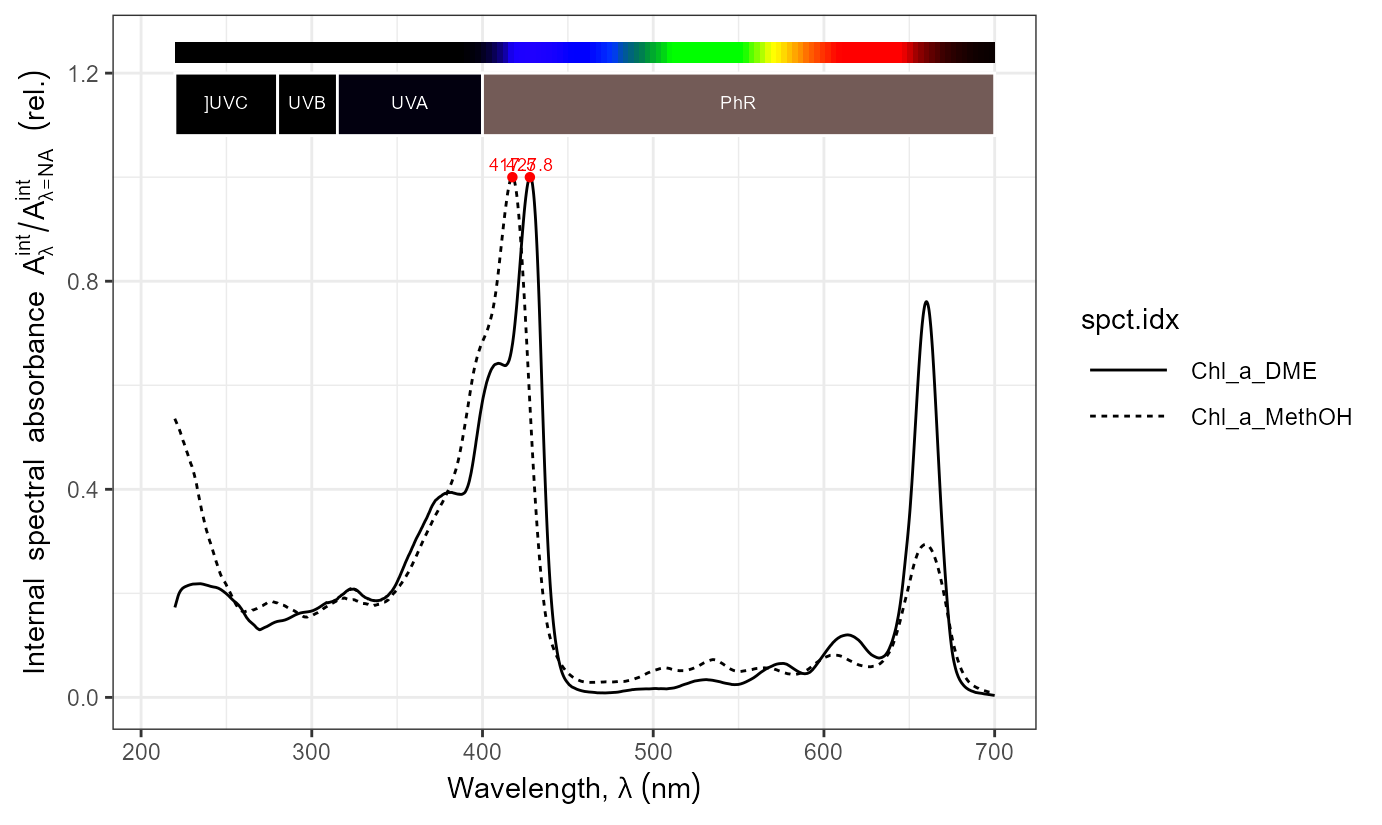
autoplot(Pfr_Ptot(300:770), unit.out = "photon",
w.band = Plant_bands(),
annotations = c("colour.guide", "labels", "boxes")) +
labs(y = "Phytochrome photoequilibrium, Pfr:Ptot ratio")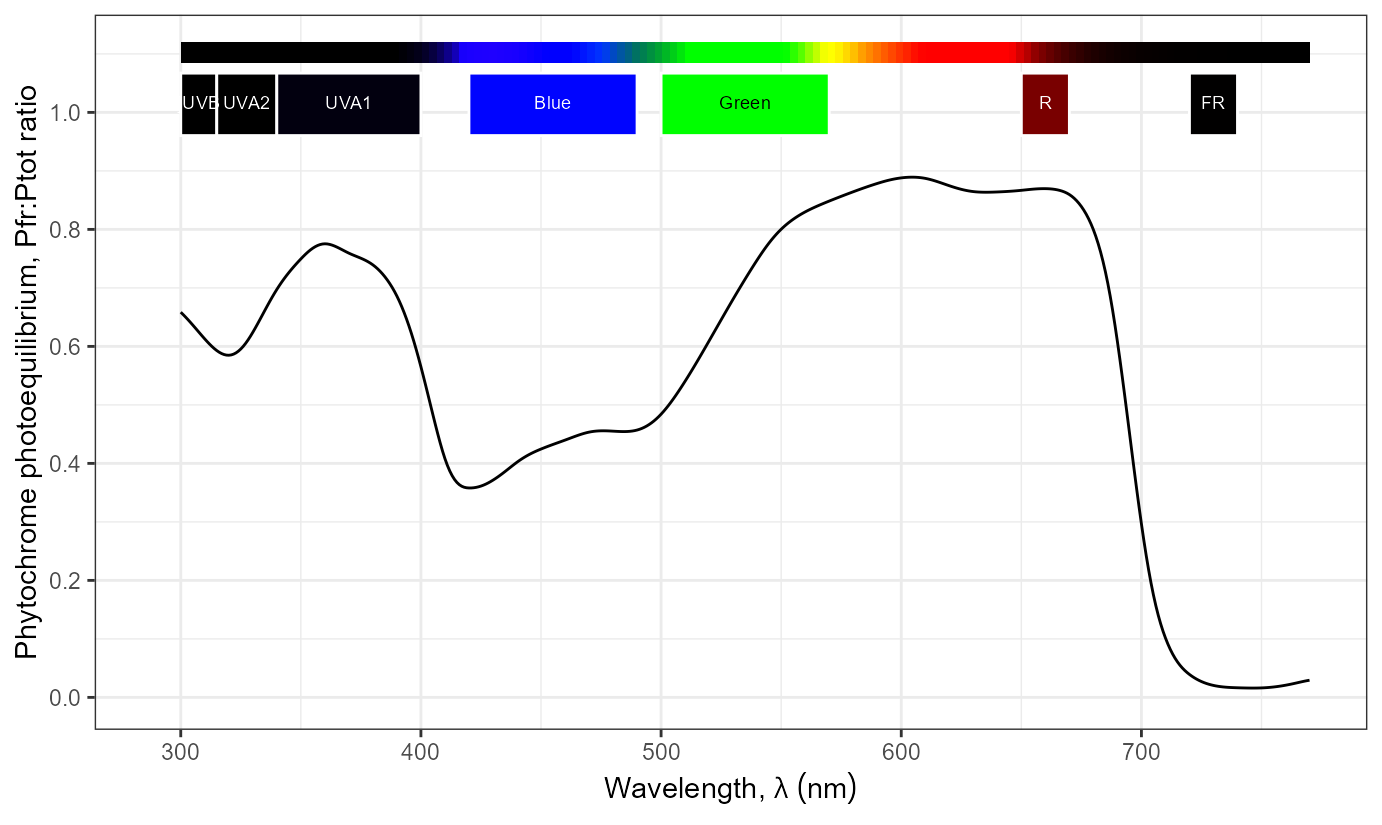
It is, of course, also possible to use base R plotting functions, or as shown here functions from package ‘ggplot2’
ggplot(data = Pfr_Ptot(300:770), aes(w.length, s.q.response)) +
geom_line() +
labs(x = "Wavelength (nm)",
y = "Phytochrome photoequilibrium, Pfr:Ptot ratio")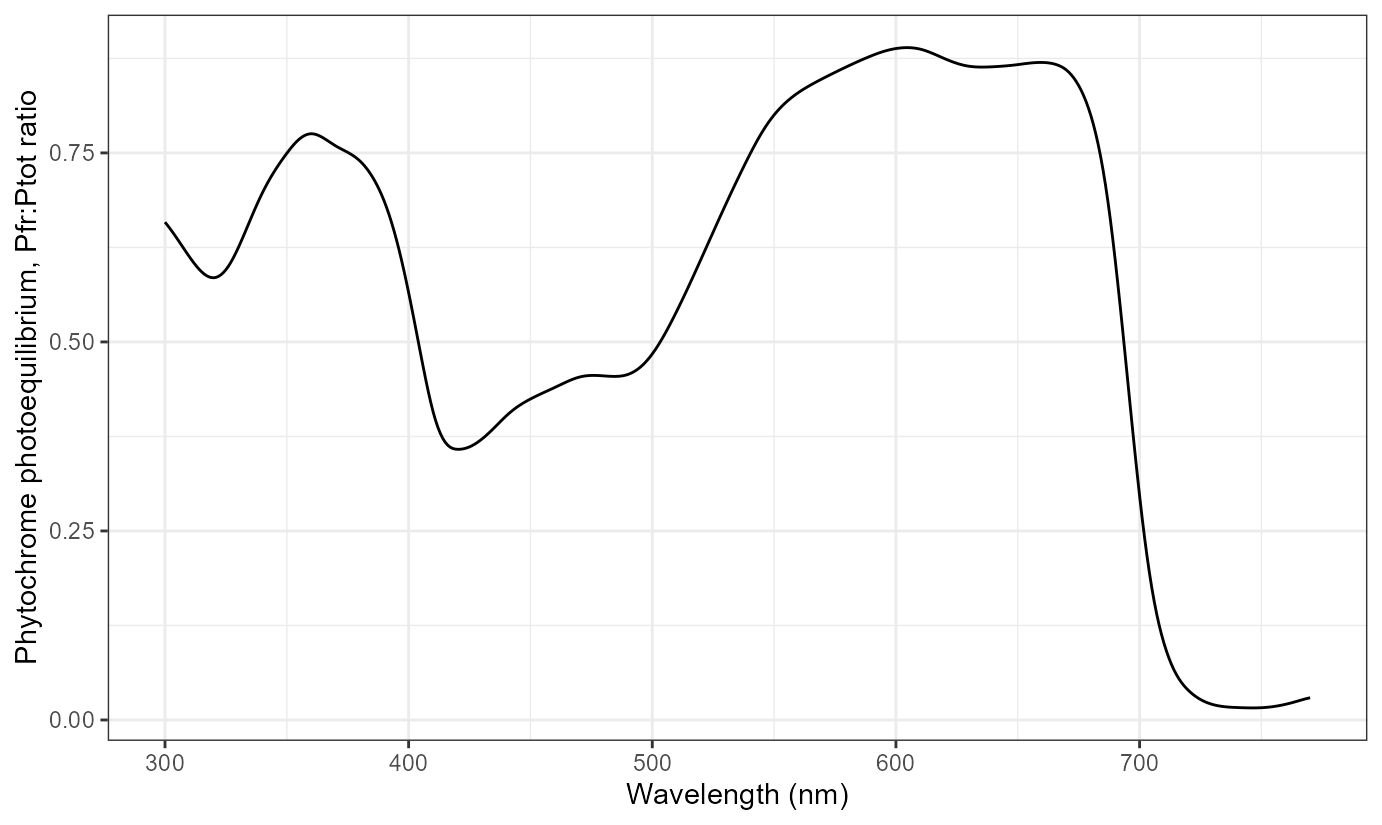
In the case of dichromatic illumination with red (660 nm) and far-red (730 nm) light, we can use a function that takes the R:FR photon ratio as argument.
These computations are valid only for true mixes of light at these two wavelengths but not valid for broad spectra like sunlight and especially inaccurate for plant growth lamps with peaks in their output spectrum, such as most discharge lamps (sodium, mercury, multi-metal, fluorescent tubes) and many LED lamps.
Pfr_Ptot_R_FR(1.15)## [1] 0.6919699
Pfr_Ptot_R_FR(0.01)## [1] 0.04747996
Pfr_Ptot_R_FR(c(1.15,0.01))## [1] 0.69196990 0.04747996It is also easy to plot Pfr:P ratio as a function of R:FR photon ratio. However we have to remember that such values are exact only for dichromatic light, and only a very rough approximation for wide-spectrum light sources. For wide-spectrum light sources, the photoequilibrium should, if possible, be calculated from spectral irradiance data.
ex6.data <- data.frame(r.fr=seq(0.01, 5.0, length.out=100), Pfr.p=numeric(100))
ex6.data$Pfr.p <- Pfr_Ptot_R_FR(ex6.data$r.fr)
ggplot(data=ex6.data, aes(r.fr, Pfr.p)) +
geom_line() +
expand_limits(y = 0) +
labs(x ="R:FR photon ratio",
y = "Phytochrome photoequilibrium, Pfr:Ptot ratio")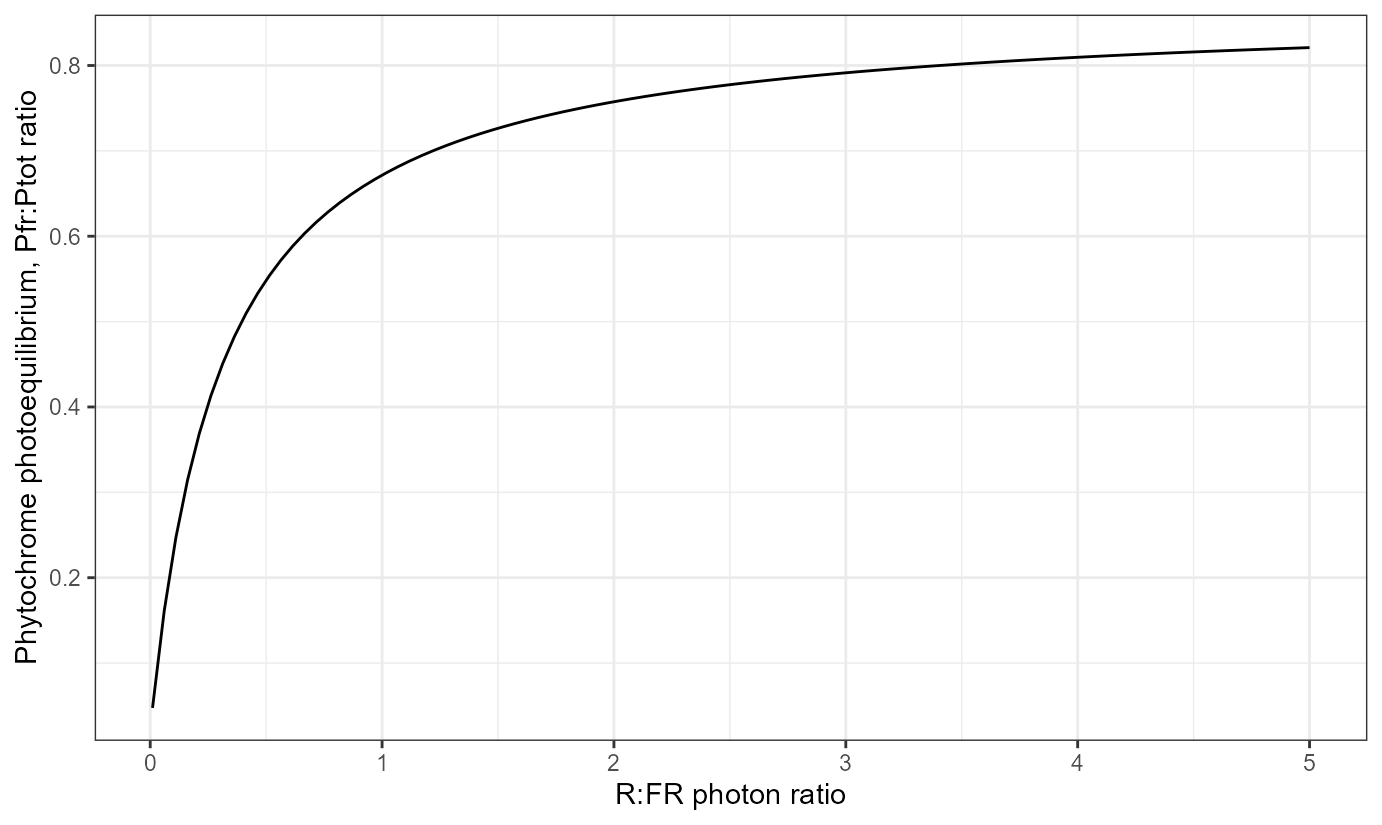
Phytochromes: reaction rates
with(clip_wl(sun.spct, c(300,770)),
Phy_reaction_rates(w.length, s.e.irrad))## $k1
## [1] 1.25935
##
## $k2
## [1] 0.5833947
##
## $nu
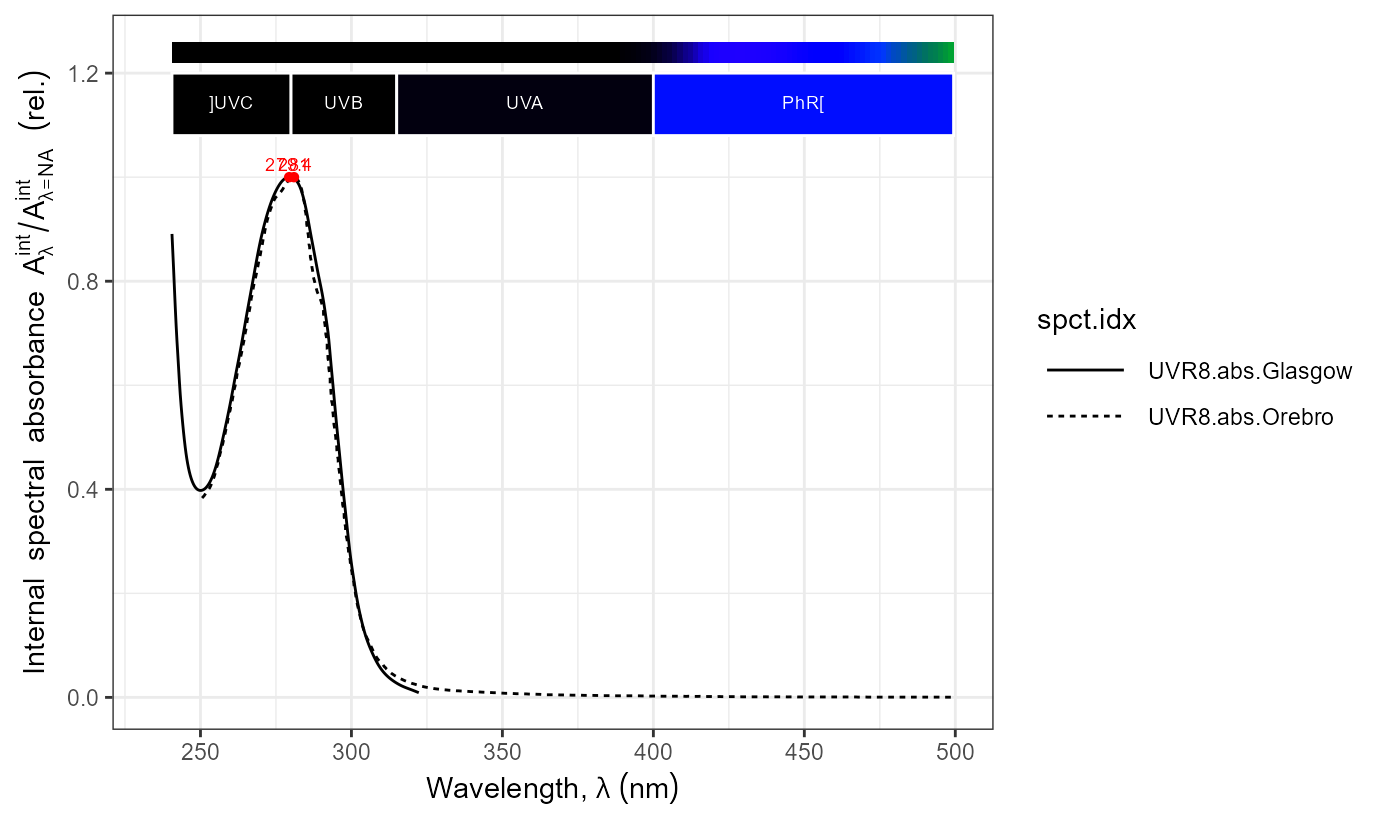
## [1] 1.842745Phytochromes: absorption cross section at given wavelengths
The phytochrome photoequilibrium cannot be calculated from the absorptance spectra of Pr and Pfr, because Pr and Pfr have different quantum yields for the respective phototransformations. We need to use action spectra, which in this context are usually called ‘absorption cross-sections’. They can be calculated as the product of absorptance and quantum yield. The values in these spectra, in the case of Phy are usually named `Sigma’.
Here we reproduce Figure 3 in Mancinelli (1994), which gives the ‘Relative photoconversion cross-sections’ of Pr (\sigma_R) and Pfr (\sigma_{FR}). The values are expressed relative to \sigma_R at its maximum at \lambda = 666 nm.
ex7.data <- data.frame(w.length=seq(300, 770, length.out=100))
ex7.data$sigma.r <- Phy_Sigma_R(ex7.data$w.length)
ex7.data$sigma.fr <- Phy_Sigma_FR(ex7.data$w.length)
ex7.data$sigma <- Phy_Sigma(ex7.data$w.length)
ggplot(ex7.data, aes(x = w.length)) +
geom_line(aes(y = sigma.r/ max(sigma.r)), colour = "red") +
geom_line(aes(y = sigma.fr/ max(sigma.r))) +
labs(x = "Wavelength (nm)", y = expression(sigma[R]~"and"~sigma[FR]))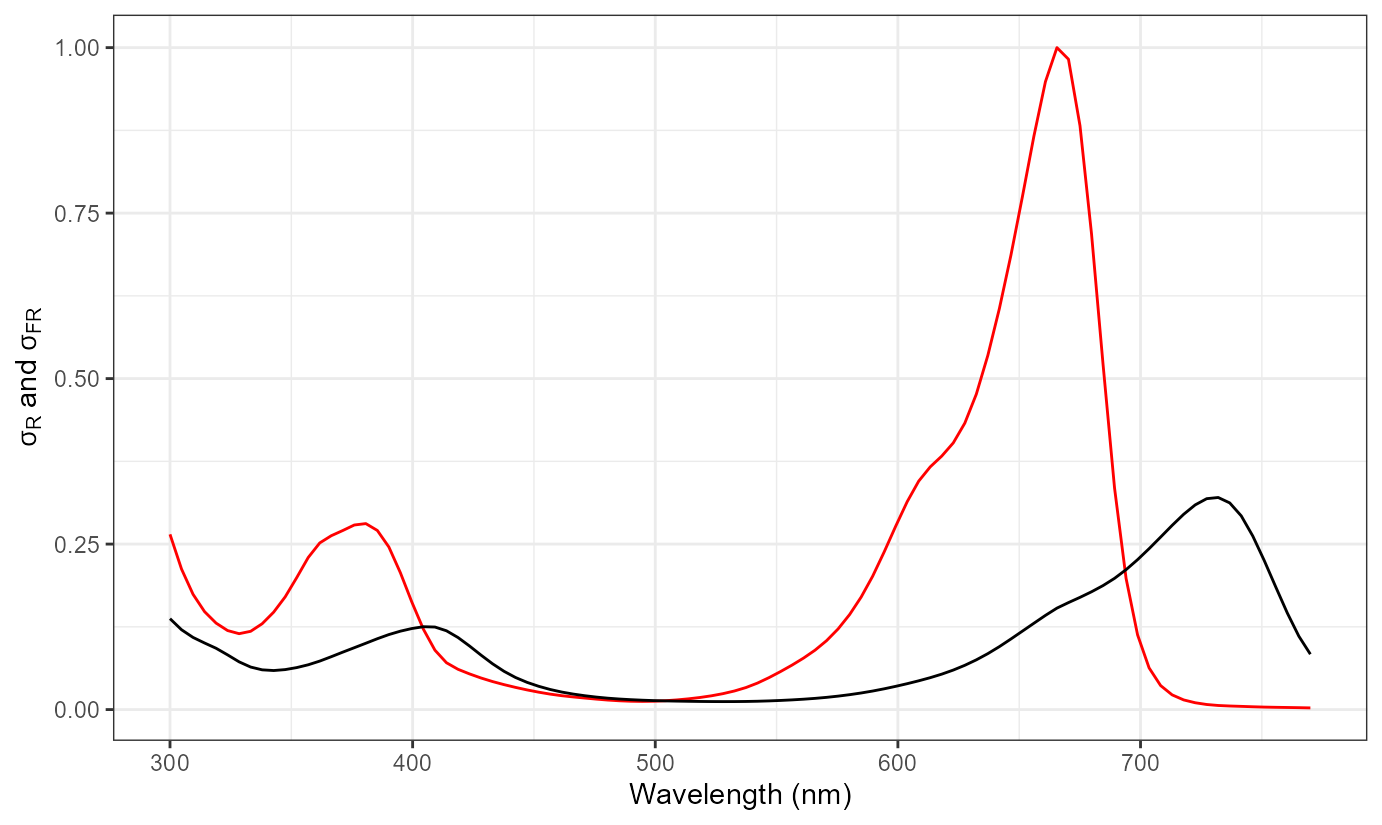
rm(ex7.data)Cryptochromes: spectral absorbance
Cryptochromes are widely distributed in plants and animals. They are blue, green and UV-A1 photoreceptors, also functioning as magneto-receptors. Their absorption spectrum depends on illumination. While the role of CRY1 and CRY2 as plant photoreceptors is well demonstrated, the role of CRY3 as a plant photoreceptor remains controversial due to the lack of evidence.
names(CRYs.mspct)## [1] "CRY1_dark" "CRY1_light" "CRY2_dark" "CRY2_light" "CRY3_dark"Here we approximate Figure 1.B from Banerjee et al. (2007).
A_as_default()
autoplot(CRYs.mspct$CRY2_dark)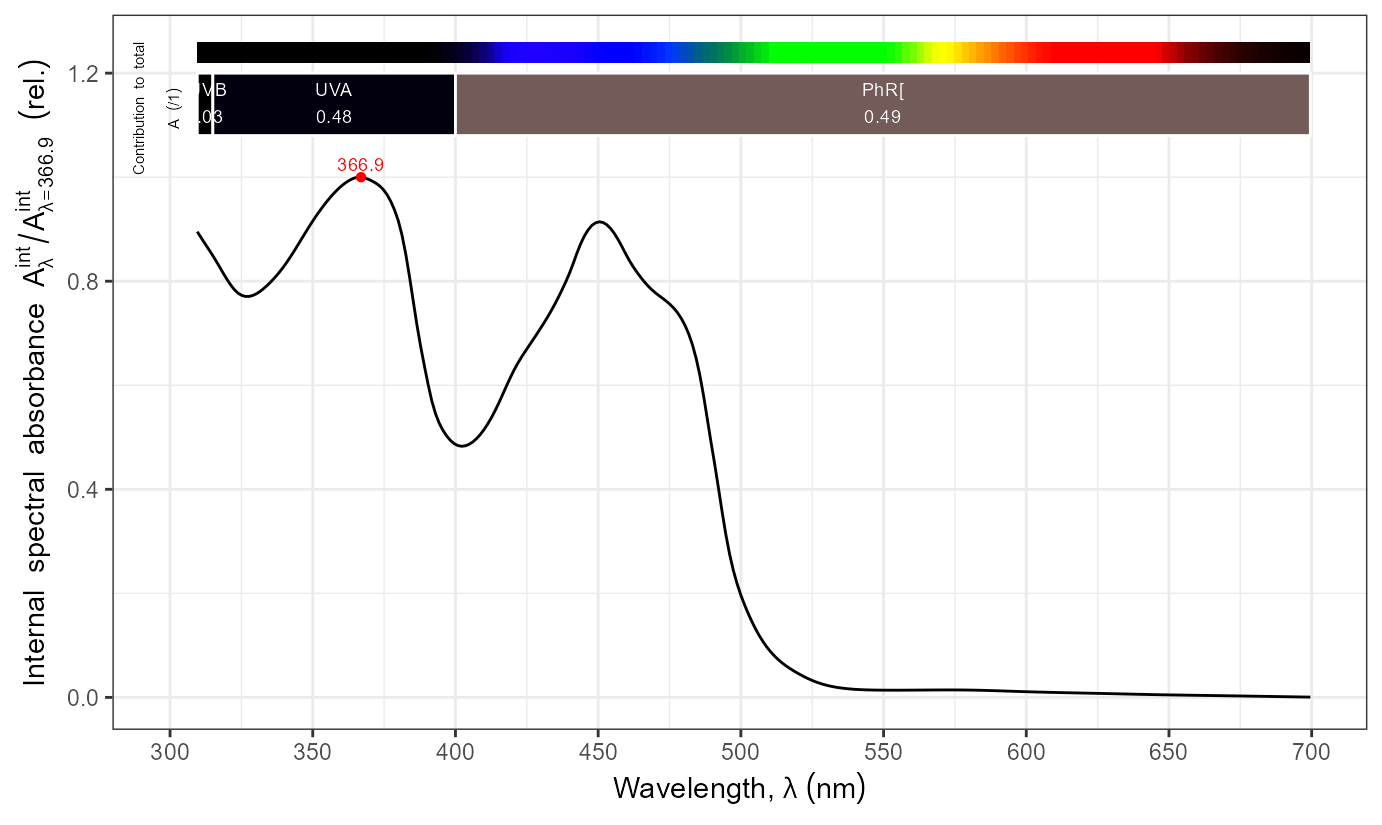
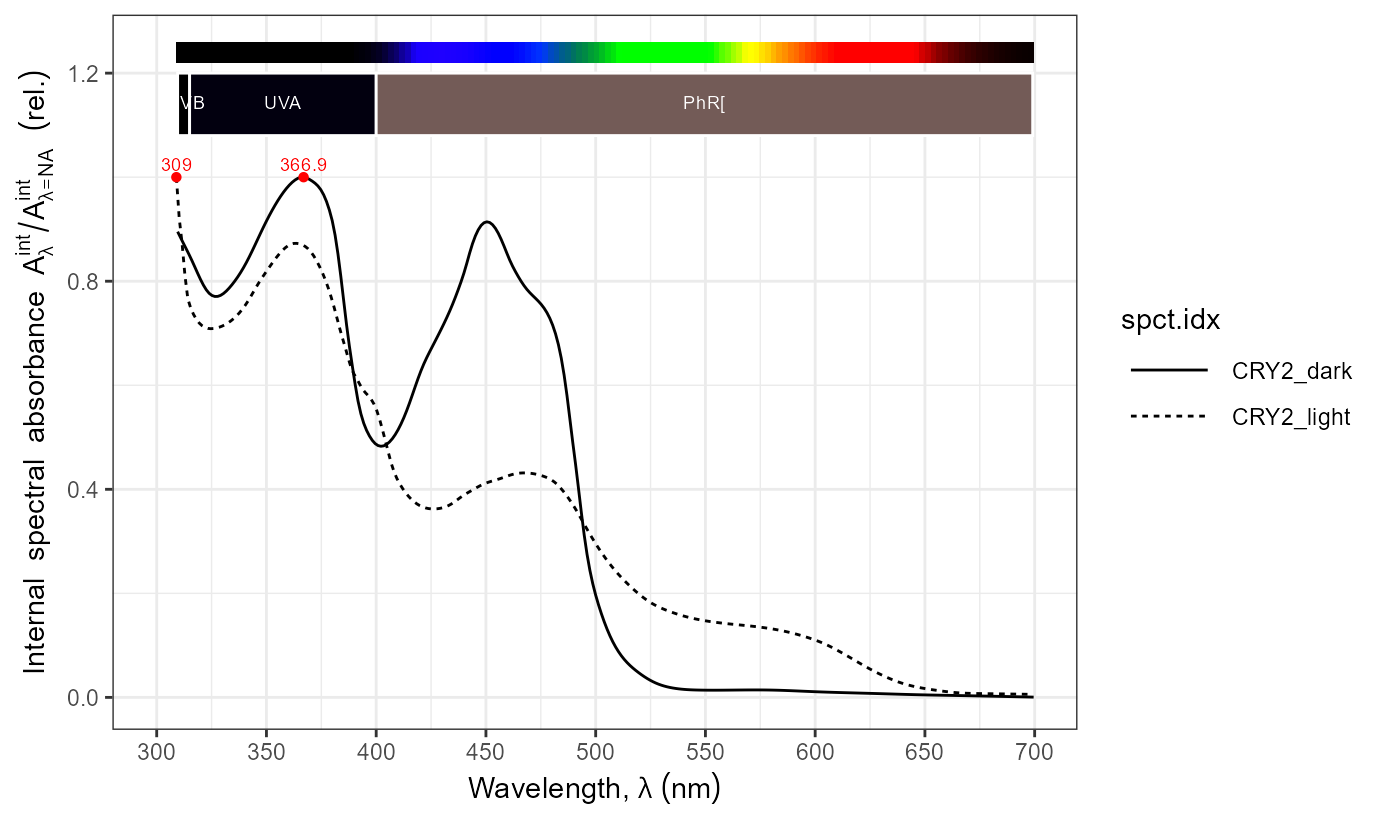
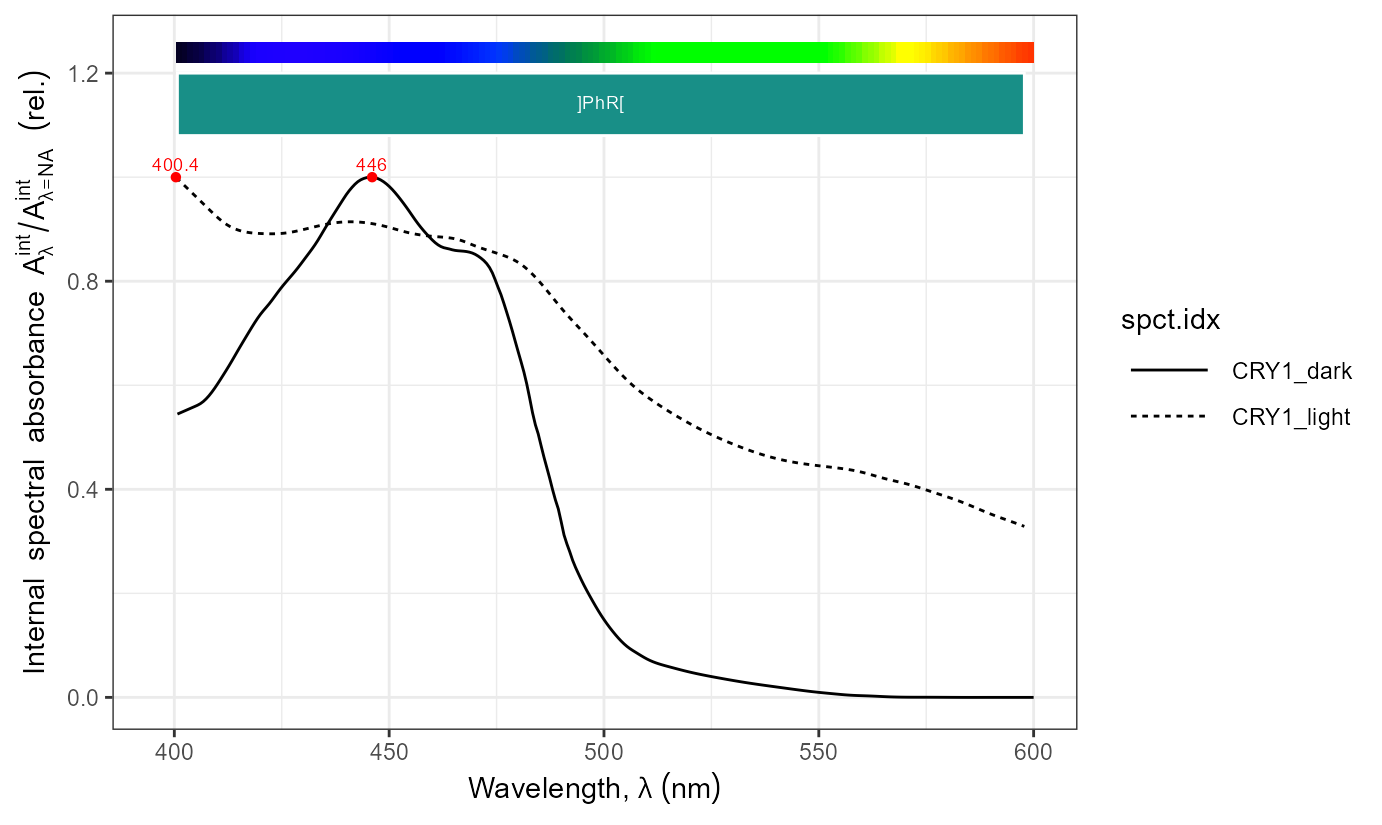
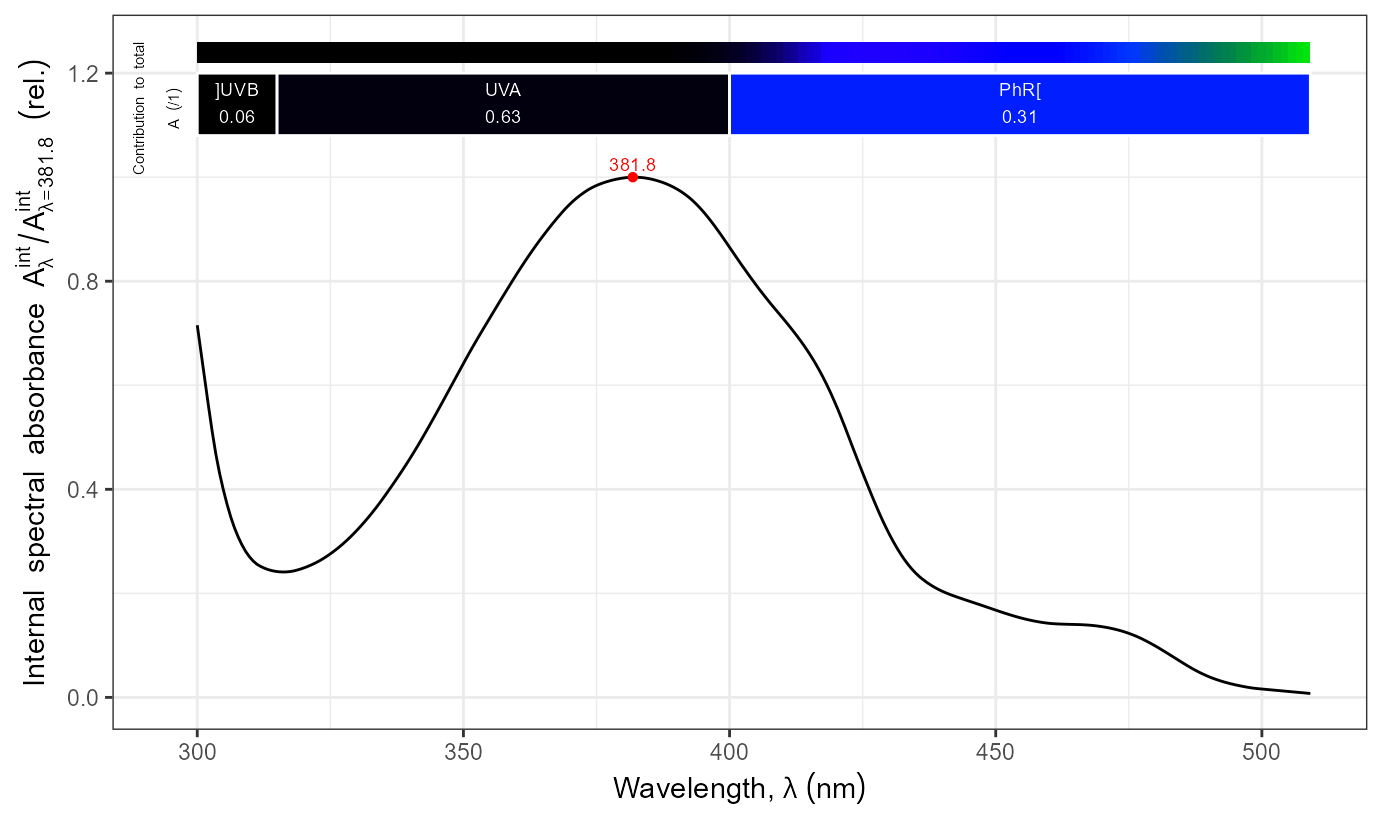
ggplot(CRYs.mspct[c("CRY1_dark", "CRY2_dark", "CRY3_dark")]) +
geom_line(aes(linetype = spct.idx)) +
expand_limits(x = 300)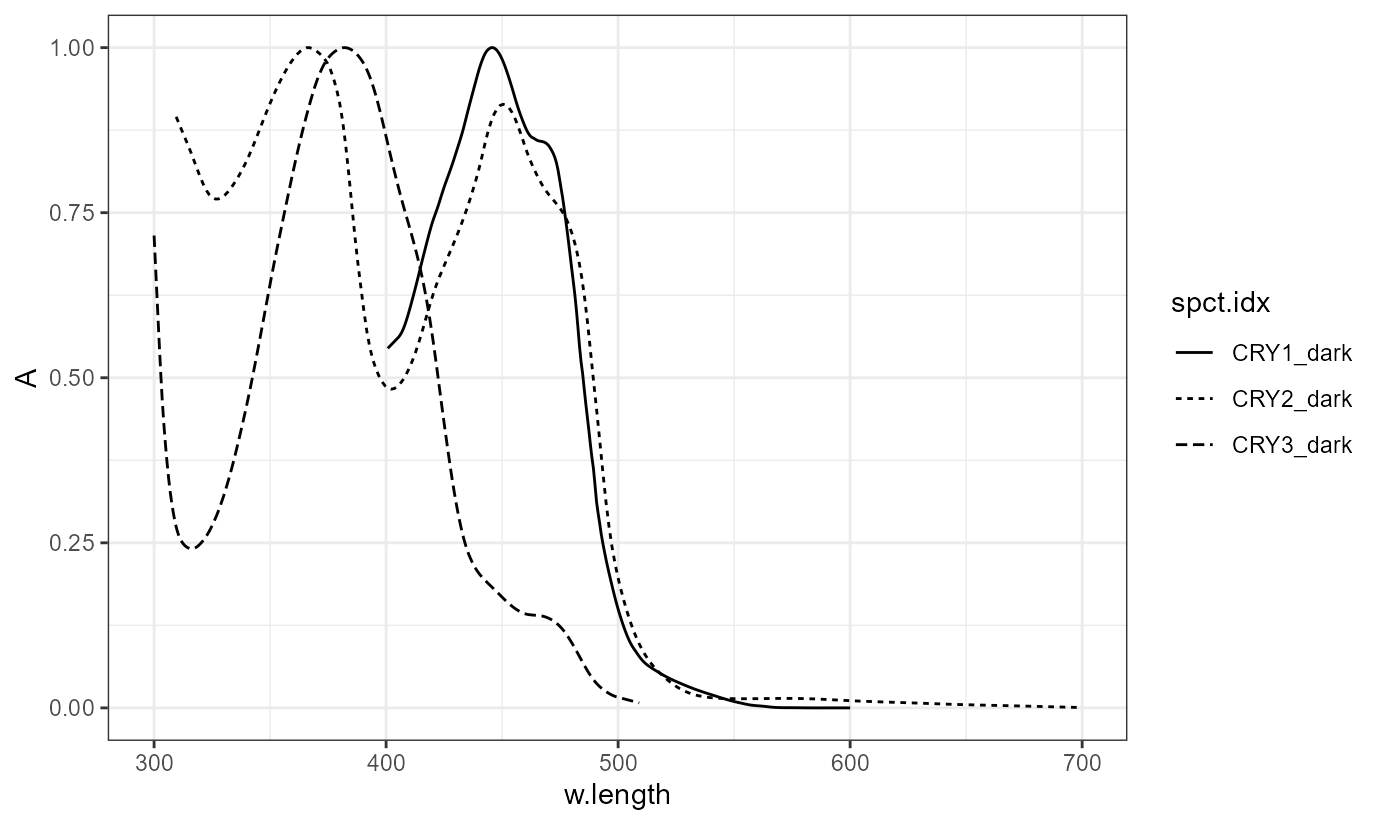
Phototropins: spectral absorbance
Phototropins are blue photoreceptors in plants, involved playing multiple roles including in phototropism (growth towards the light) and in rapid stomatal opening in response to illumination.
names(PHOTs.mspct)## [1] "PHOT1_fluo" "PHOT2_fluo" "PHOT1_dark" "PHOT1_light"
autoplot(PHOTs.mspct[c("PHOT1_fluo", "PHOT2_fluo")]) +
expand_limits(x = 300)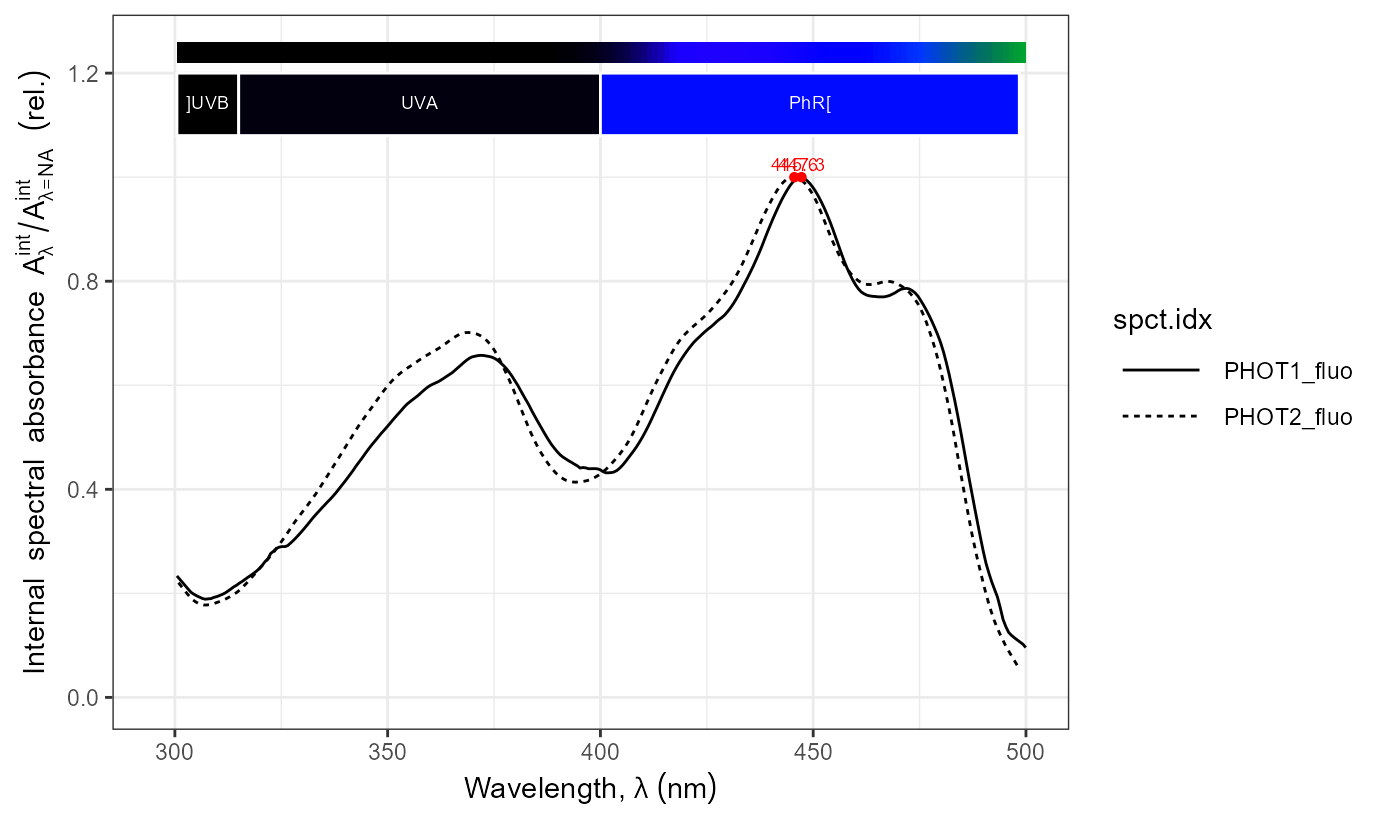
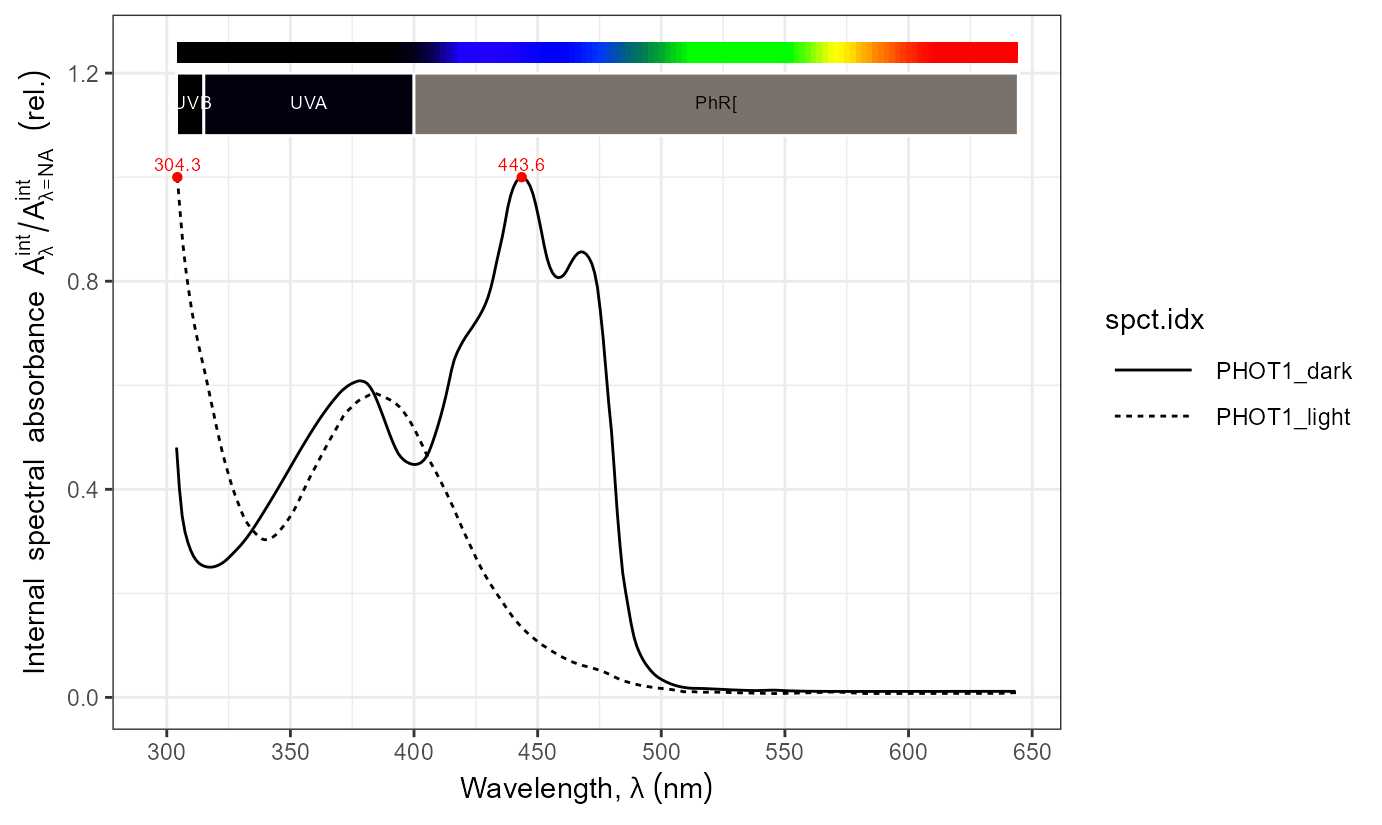
UVR8: spectral absorbance
UVR8 is a plant photoreceptor sensitivy to UV-B radiation. However, in sunlight because of the shape of the terrestrial spectrum of sunlight, it plays the role of an UV-B and UV-A2 receptor.
autoplot(UVR8s.mspct)## Discarding heterogeous 'filter.descriptor' attributes!!
Zeitloupe proteins: spectral absorbance
This proteins are blue photoreceptors playing an important role in reproductive induction of plants.
names(ZTLs.mspct)## [1] "ZTL_dark" "ZTL_light"
autoplot(ZTLs.mspct) +
expand_limits(x = 300)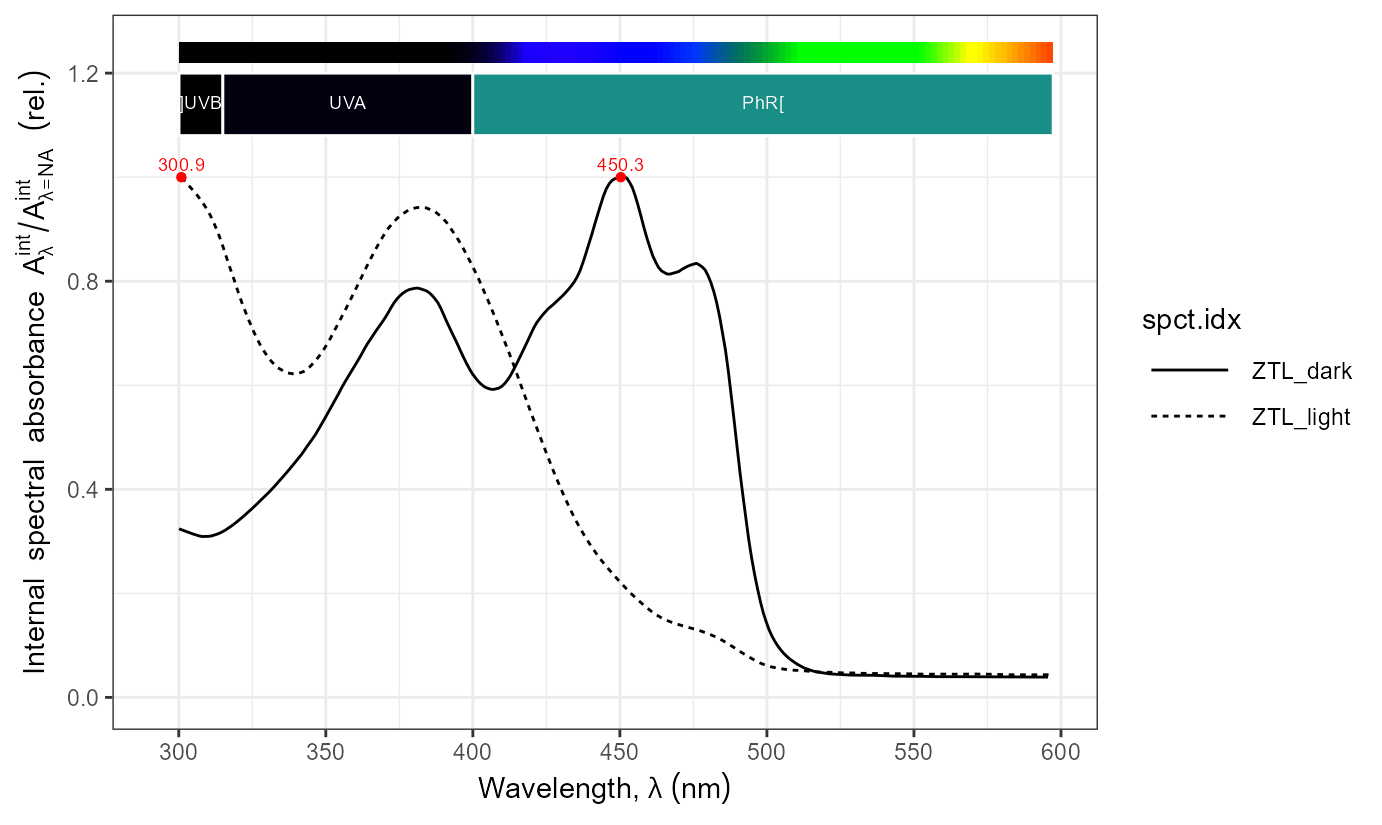
Mass pigments
The term mass pigments is used to describe light absorbing molecules that absorb significant amount of the light or ultraviolet radiation inpinging on plants. They not only are inheritently good absorbers of radiation but are present in plant tissues at relatively high concentrations. Some like carotenoids play both a role in energy harvesting and in protection from excess energy. Chlorophylls main role is in energy harvest and that of flavonoids, cinnamic acids and other phenolics located in the epidermis mainly function as screens that protect the inner tissues of the leaves from excess radiation, especially UV. These spectra have been measured after extracting the pigments.
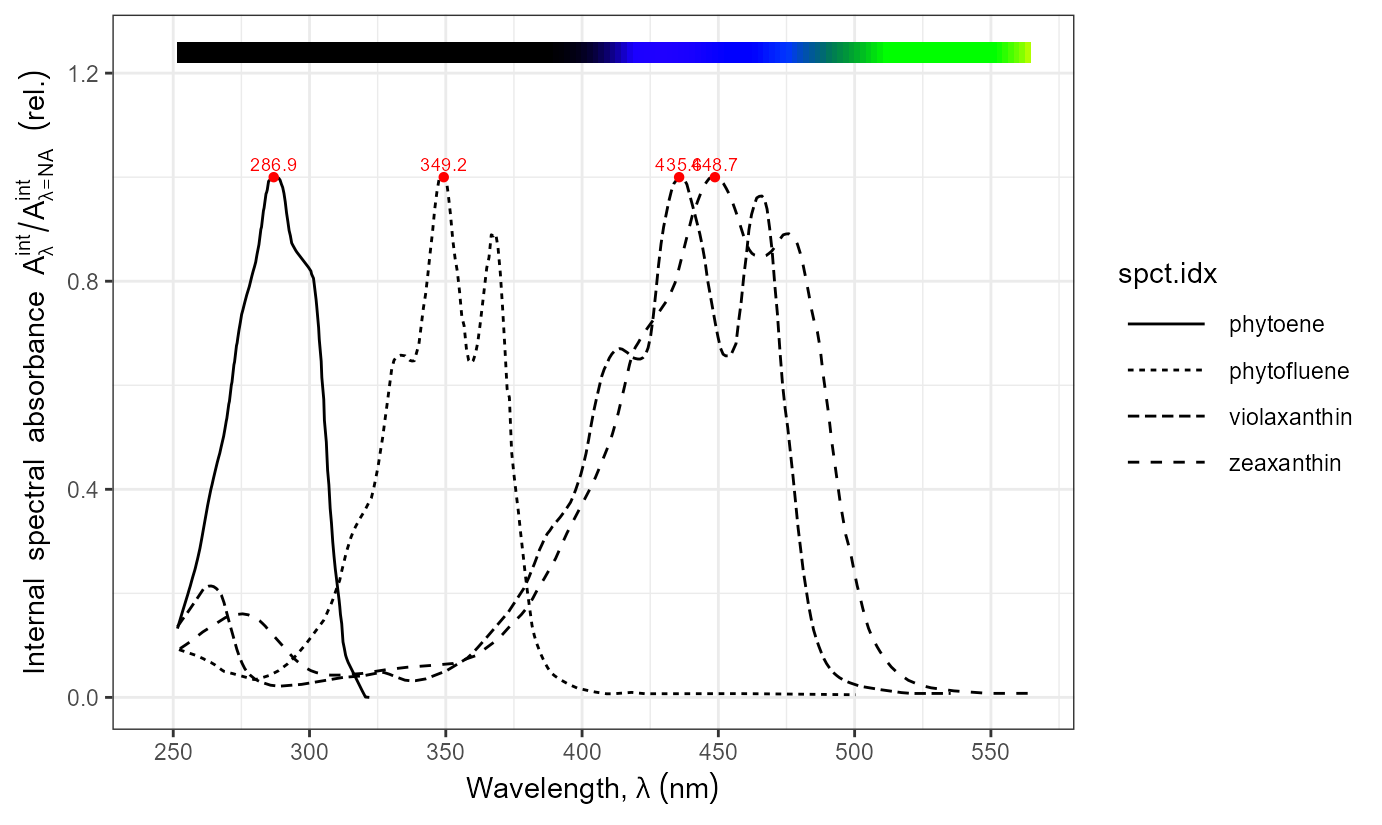
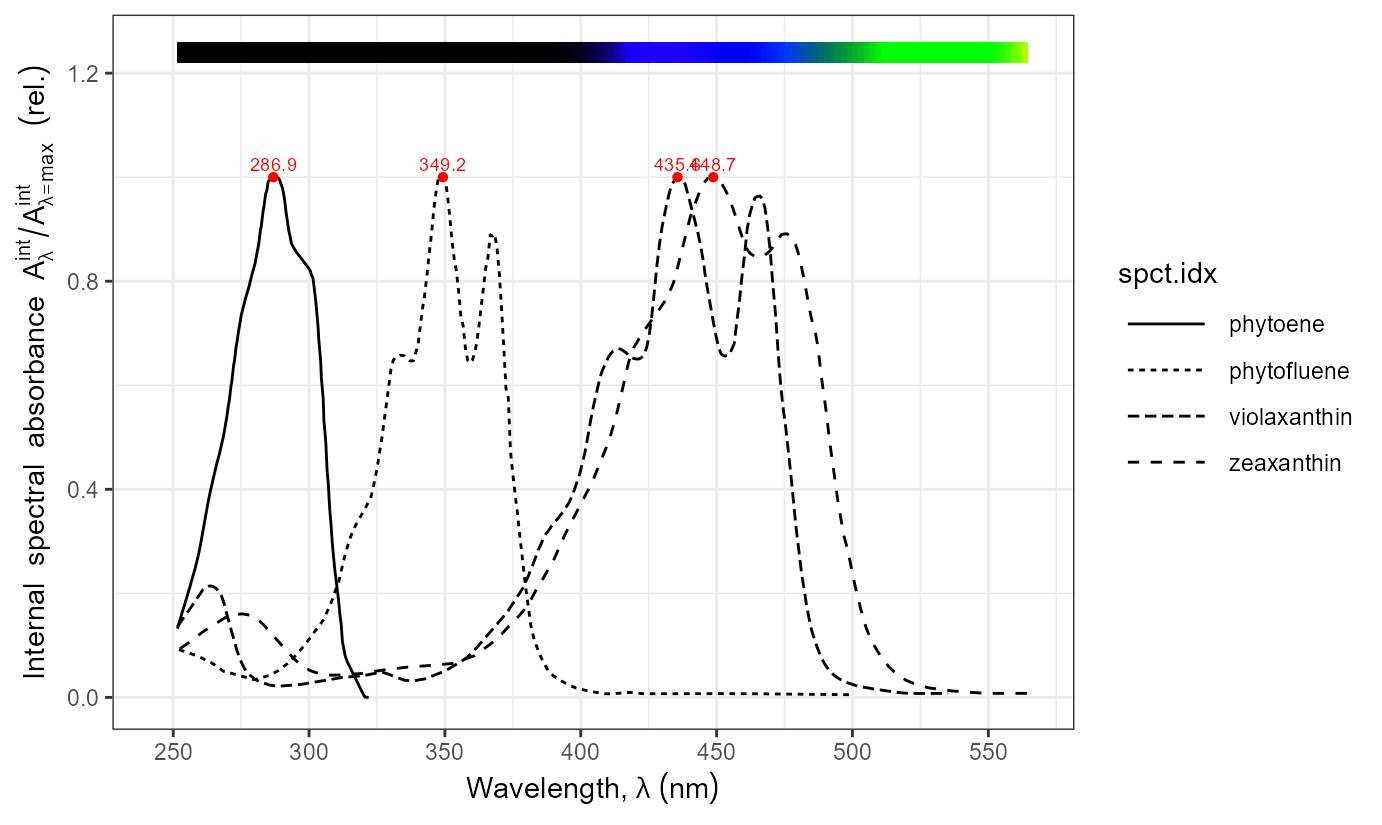
Carotenoids
names(carotenoids.mspct)## [1] "beta_carotene" "dihydro_lycopene" "lycopene" "lutein"
## [5] "phytoene" "phytofluene" "violaxanthin" "zeaxanthin"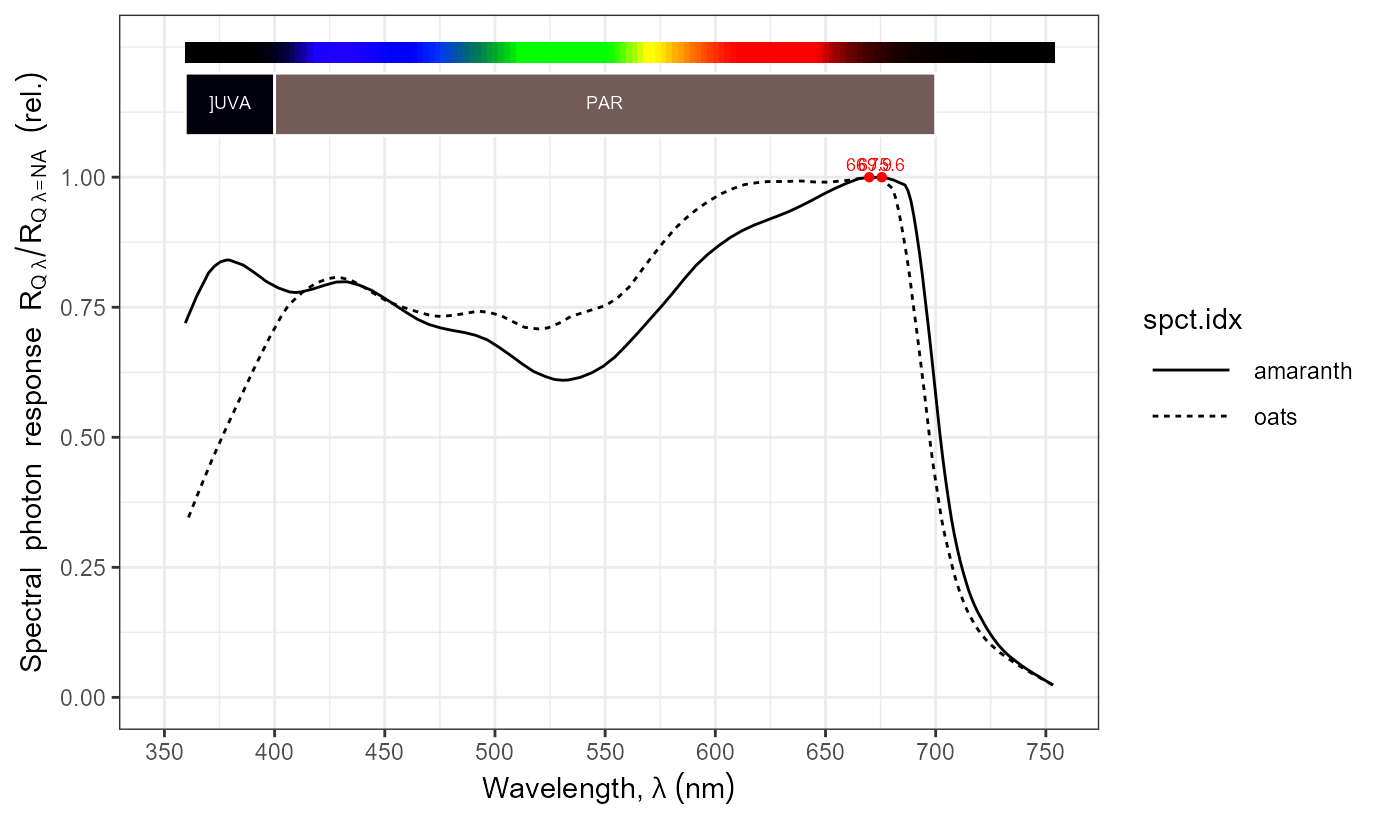
Leaves
Optical properties
The optical properties of leaves depend on the pigments the contain and on the anatomical structure of leaf tissues. In addition to absorption by pigments, light scattering within the leaf plays a central role. Scattering alters the route photons take within leaves increasing absorption and altering the shape of the absorption spectrum.
names(Solidago_altissima.mspct)## [1] "lower_adax" "lower_abax" "upper_adax" "upper_abax"
autoplot(Solidago_altissima.mspct$lower_adax) 
autoplot(Solidago_altissima.mspct$lower_abax)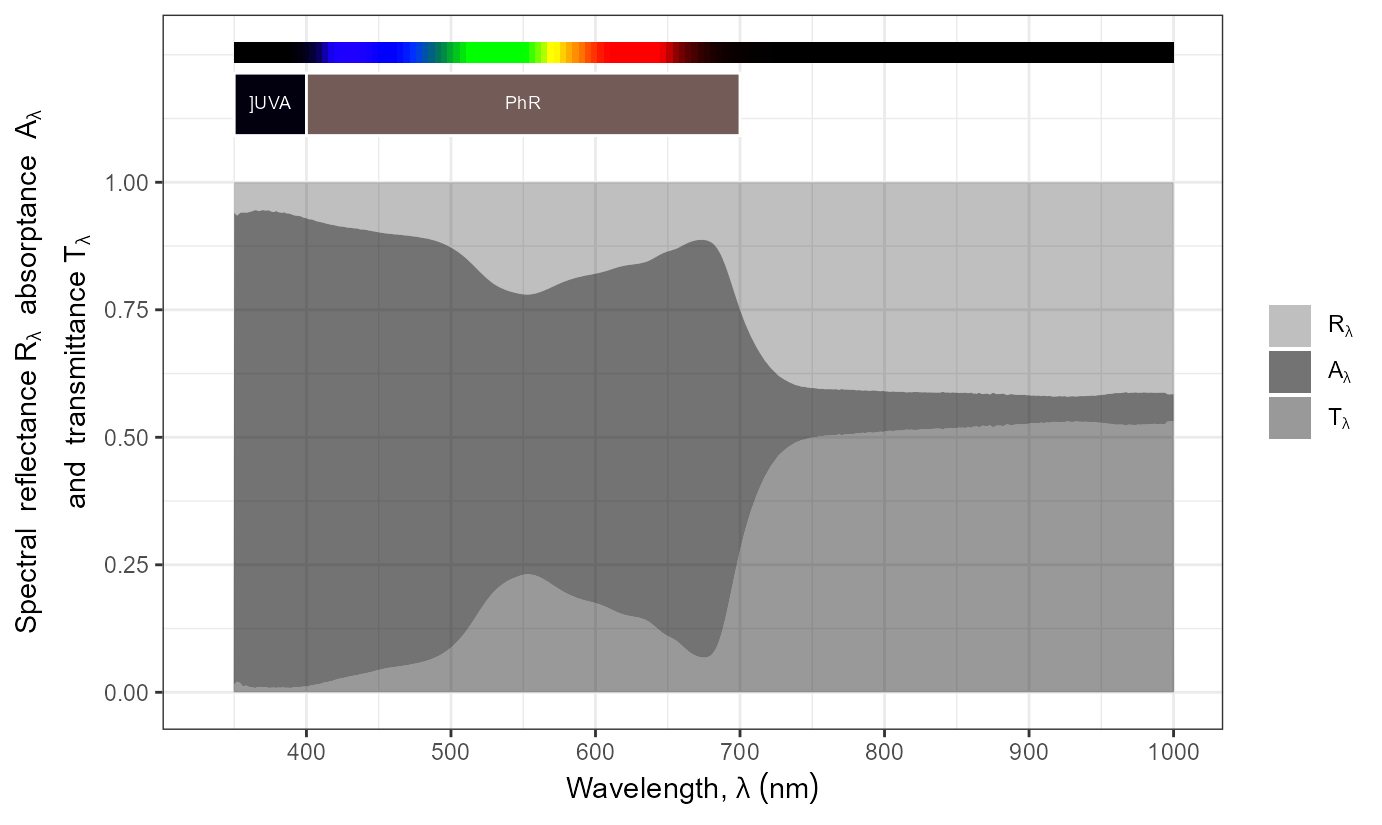 
autoplot(as.filter_mspct(Betula_ermanii.mspct))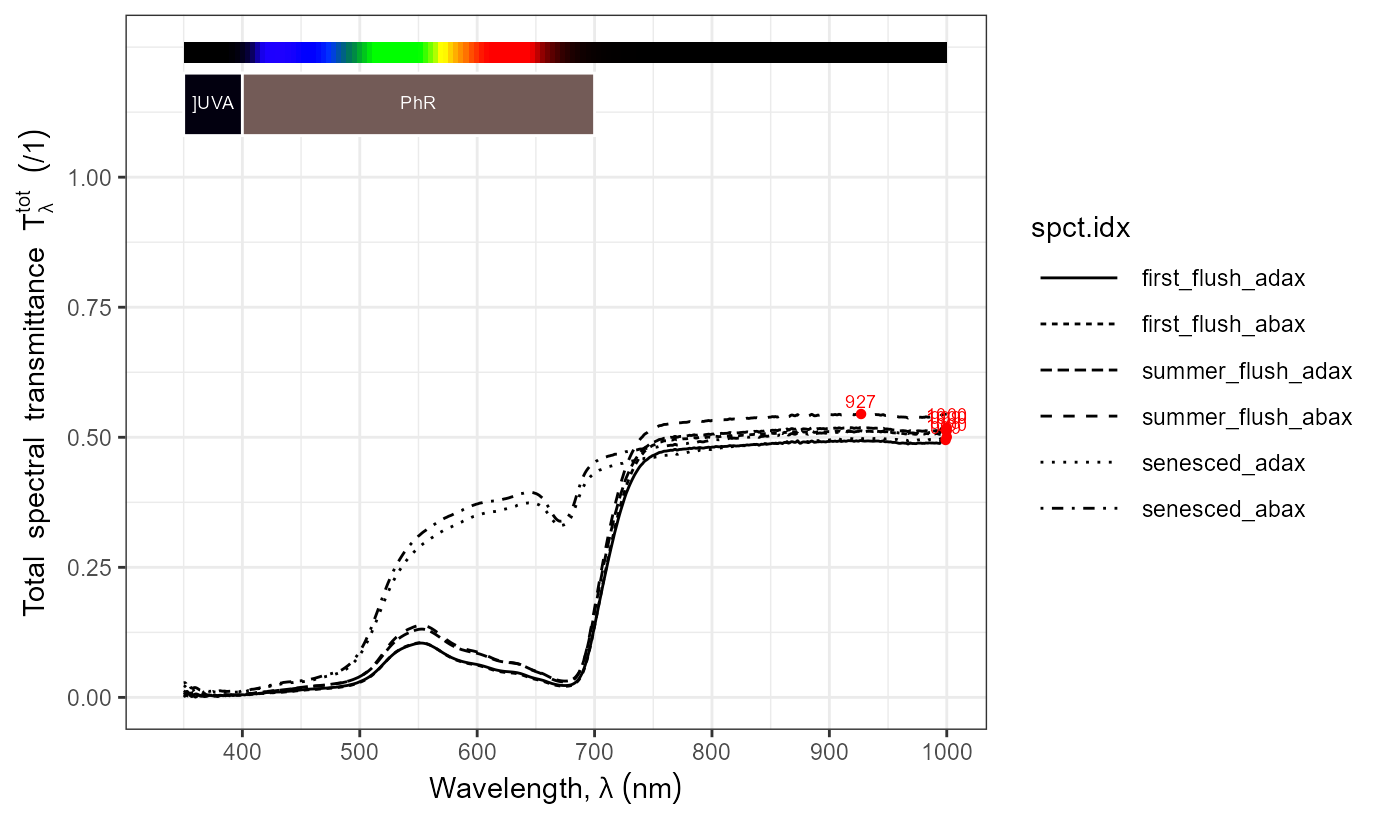 
autoplot(as.reflector_mspct(Betula_ermanii.mspct))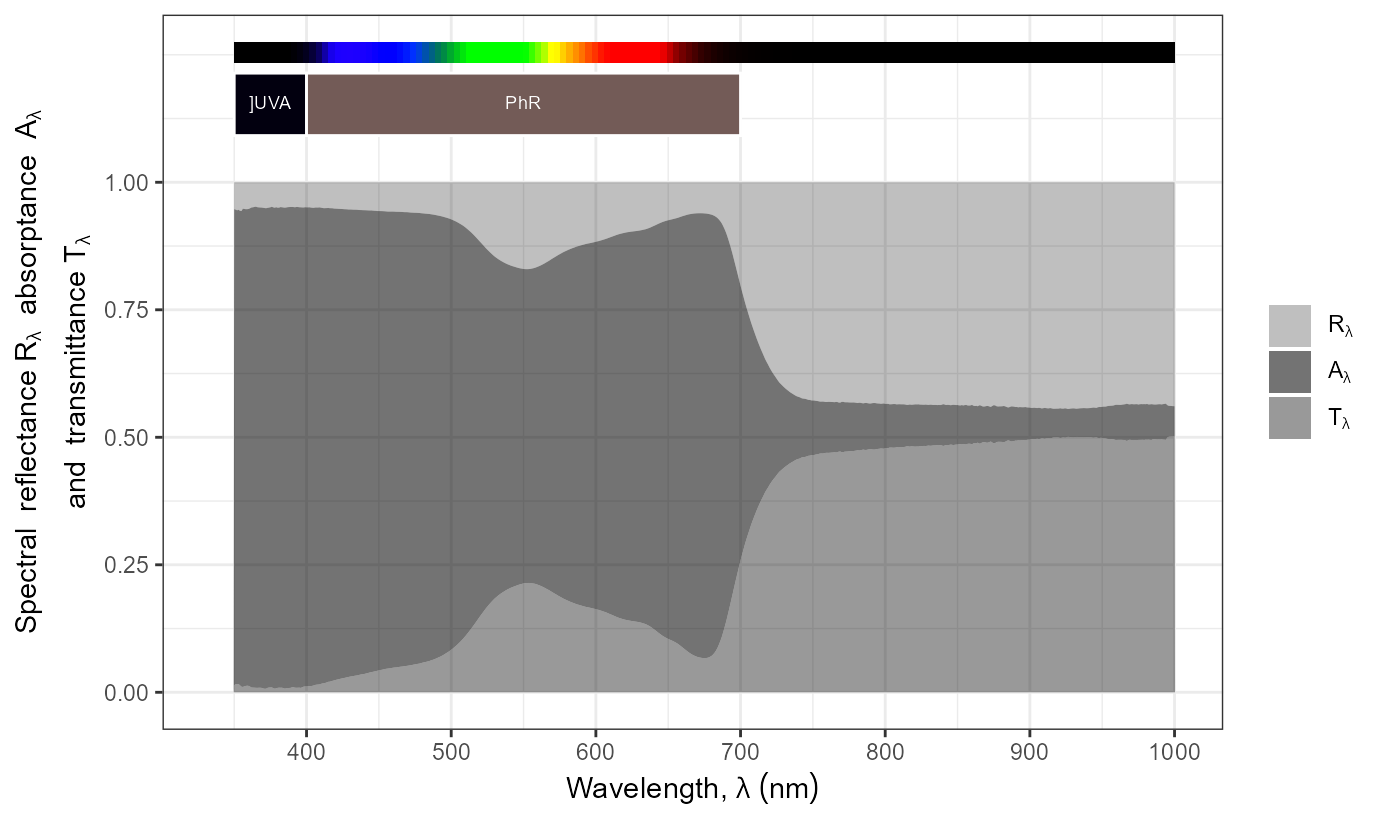 
Fluorescence: UV excited
Pigments excited by the absorption of photons, release part of this energy as photons of lower energy, i.e., longer wavelength. The wavelengths of the emitted fluorescence is determined by the allowed energy states of electrons in molecules. The most obvious fluorescence in plants is the red fluorescence from chlorophylls. Leaves containing cinnamic acids in the epidermic, such as many grasses and sunflower, in addition to red fluorescence, usually emit blue and sometimes cyan fluorescence. Chlorophylls a and b differ in their spectra, emitting red fluorescence centred around two nearby but distinct wavelength.
names(leaf_fluorescence.mspct)## [1] "wheat_Fo_ex355nm"
autoplot(leaf_fluorescence.mspct$wheat_Fo_ex355nm,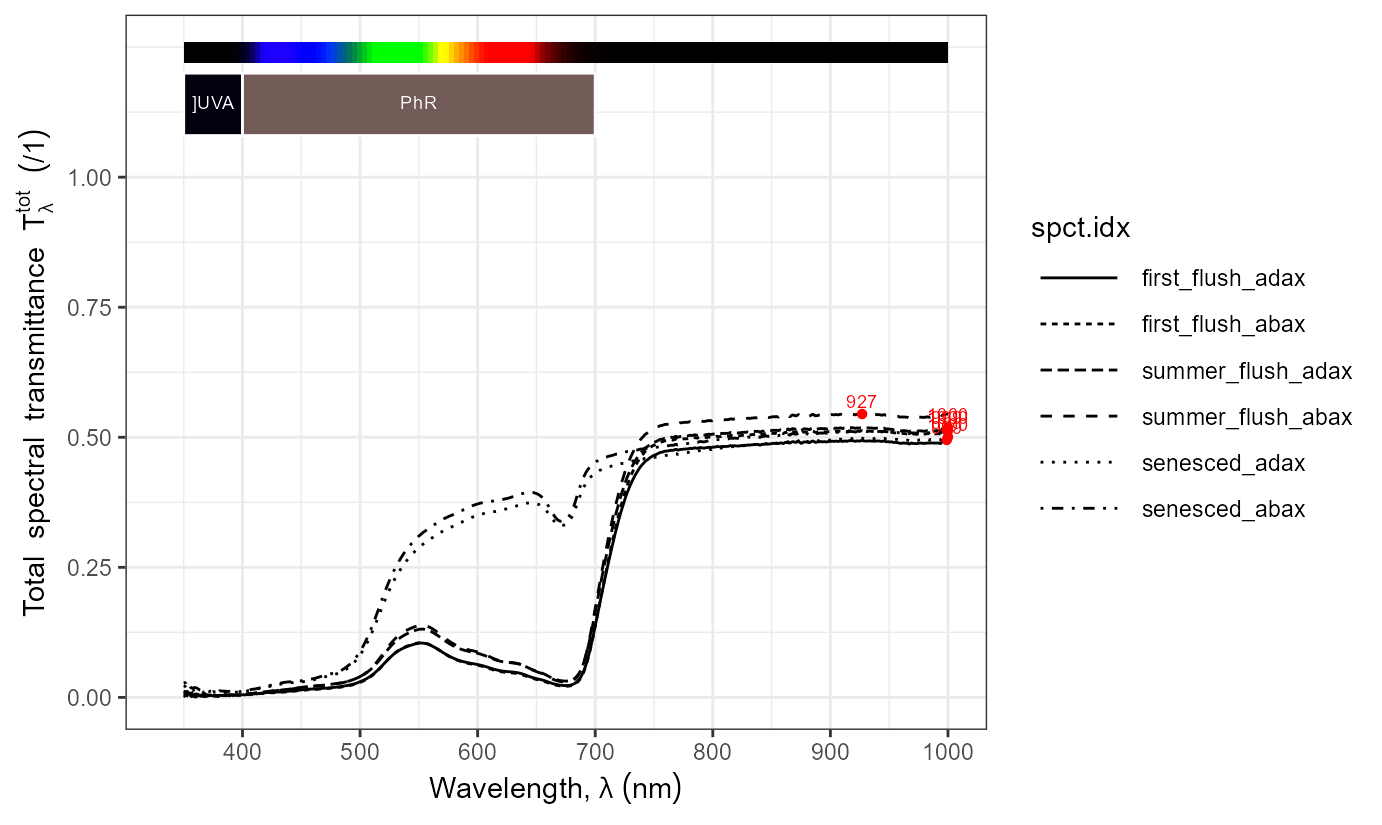
span = 21)
Photosynthesis: action spectra
The action spectrum of leaf photosynthesis differs from both the absorption spectra of the pigments and of whole leaves. One reason is that the effectiveness with which absorbed photons of different wavelengths drive electron transport is not the same. Furthermore, the response of photosynthesis to irradiance is not linear. Different species, differ in pigment concentrations and localization, anatomy and metabolic capacity.
names(McCree_photosynthesis.mspct)## [1] "amaranth" "oats" "lettuce"
autoplot(McCree_photosynthesis.mspct)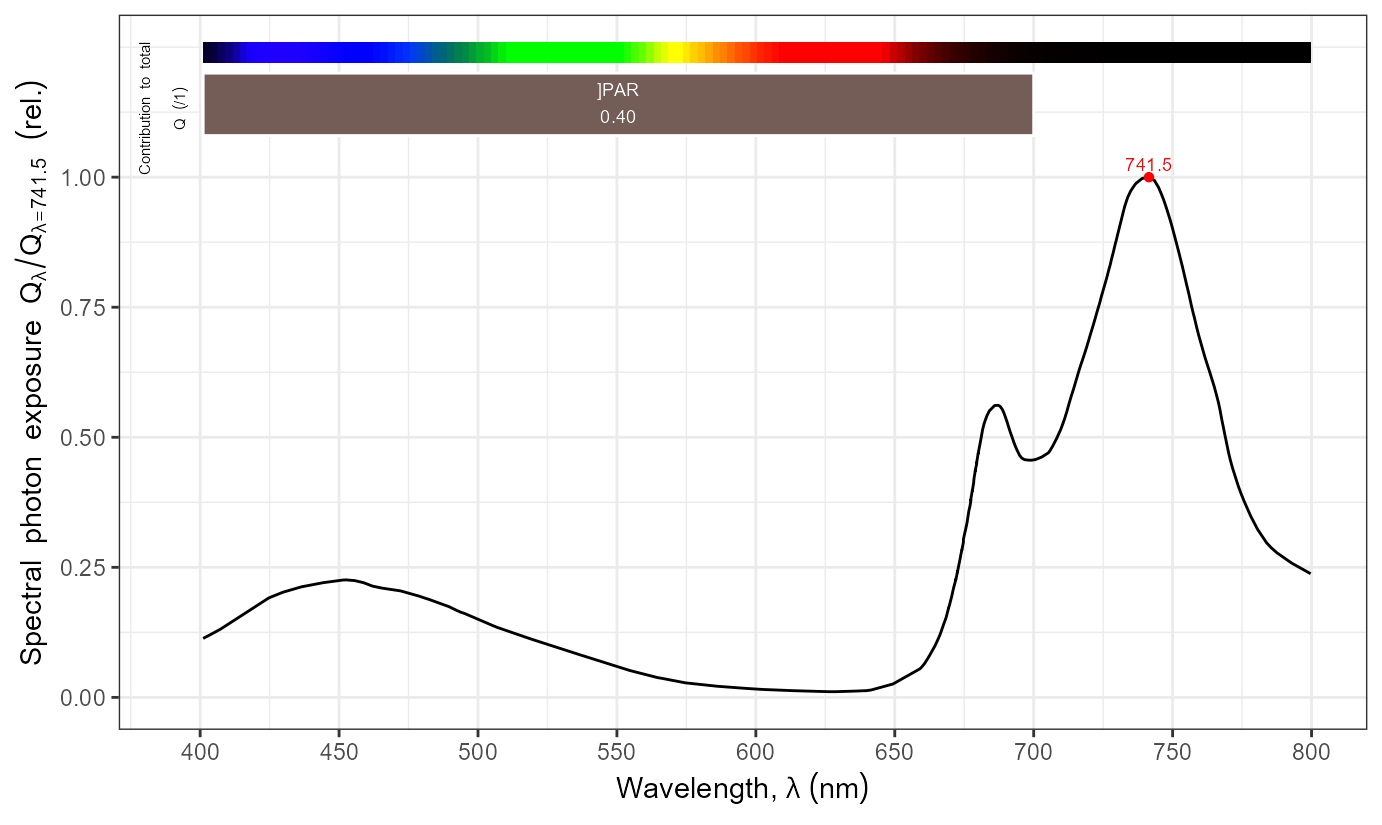
Photosynthesis: plastoquinone redox state
The balance between the activation of photosystem 1 (PSI) and photosystem 2 (PSII) depends on the wavelengths of the incoming radiation as the chlorophylls in the two photosystems absorb predominantly at different wavelengths. The balance between PSI and PSII affects the redox state of the plastoquinone pool. Based on a published model fitted to measured state of the pool under different light sources makes it possible to guesstimate how a given light source can affect the redox state. This model can be used, with care, to assess light from different sources in relation to its ability to drive PSI relative to PSII. The actual balance between PSI and PSII acclimates and in addition depends on plant species, genotype and plant growing conditions!
PQ_redox_state(sun.spct) # % in reduced state## [1] 26.17694
PQ_redox_state(sun.spct, attr2tb = "when.measured")## # A tibble: 1 × 3
## spct.idx PQ_redox.state when.measured
## <fct> <dbl> <dttm>
## 1 spct.name 26.2 2010-06-22 09:51:00Stomatal conductance
The functions described in this section are available in ‘photobiologyPlants’ (>= 0.6.2).
While in meteorology it is common to use stomatal resistances expressed based of volume, in plant sciences their expression as molar conductances is the norm. The conversion depends on the molar volume of air, which here is treated as an ideal gas. The molar volume is a function of temperature and pressure.
1 / gs_mol2vol(0.150) # mol m-2 s-1 -> s m-2## [1] 276.1464
# mol m-2 s-1 -> s m-2
1 / gs_mol2vol(0.150, temperature = 5, pressure = 98e3) ## [1] 282.5177Stomatal conductance is directly dependent on the diffusion coefficient (D) which depends on the chemical species, temperature and pressure.
gs_c_from_gs_w(0.150) # mol m-2 s-1## [1] 0.09109934Estimation of stomatal conductance from the measured size of the stomatal pore is challenging, both because of the difficulty in doing the measurements and because the equation used is based on an approximation to the real shape of stomata.
gs_w <-
gs_w_from_size(length = 10e-6, # m
width = 5e-6, # m
depth = 20e-6, # m
n = 50e6, # m^-2 (stomatal density)
temperature = 30) |> # C
gs_vol2mol(temperature = 30, pressure = 101e3) # C, Pa
gs_w # for water vapour mol m-2 s-1## [1] 0.09914633
gs_w * 1e3 # for water vapour mmol m-2 s-1## [1] 99.14633
gs_c_from_gs_w(gs_w) * 1e3 # for CO2 mmol m-2 s-1## [1] 60.21443These functions rely on computation of the volumetric diffusion coefficients,
## [1] 2.12e-05 2.27e-05 2.42e-05 2.57e-05 2.72e-05## [1] 1.29e-05 1.38e-05 1.47e-05 1.56e-05 1.65e-05and the molar volume of an ideal gas.
## [1] 0.02241825 0.02323898 0.02405971 0.02488045 0.02570118## [1] 0.02529407 0.02478819 0.02430215Vegetation
The functions described in this section have been migrated from package ‘photobiology’ (>= 0.12.0) to ‘photobiologyPlants’ (>= 0.6.0).
Reference evapotranspiration
Evapotranspiration is the combined water fluxes between a vegetation canopy and the atmosphere, It is the sum of transpiration (water that evaporates inside leaves and flows through stomata) and evaporation (water that evaporated from the soil and other surfaces, including from the wet outer surfaces of plants and their leaves). Measured evapotranspiration is described as actual evapotranspiration (\mathrm{ET}), the maximum rate of evapotranspiration of short vegetation canopy is called reference evapotranspiration (\mathrm{ET}_\mathrm{ref}), also described as potential evapotranspiration (\mathrm{PET})). Potential evapotranspiration can be measured on irrigated vegetation, but can also be estimated from meteorological conditions. Supported methods are the current FAO recommended and some earlier ones still in use.
Instantaneous \mathrm{ET}_\mathrm{ref} expressed in mm\ h^{-1} can be obtained with
ET_ref().
ET_ref(temperature = 20, # C
water.vp = water_RH2vp(relative.humidity = 70, # RH%
temperature = 20), # C -> Pa
wind.speed = 0, # m s-1
net.irradiance = 100) # W m-2## [1] 0.172792Daily \mathrm{ET}_\mathrm{ref}
expressed in mm\ d^{-1} can be obtained
with ET_ref_day()
ET_ref_day(temperature = 20, # C daily mean
water.vp = 1636.616, # Pa daily mean
wind.speed = 5, # m s-1 daily mean
net.radiation = 15e6) # 15 MJ / d / m2 daily total !## [1] 7.199597As many of other factions in the package, these functions are vectorized.
ET_ref(temperature = 20, # C
water.vp = water_RH2vp(relative.humidity = (1:9) * 10, # RH%
temperature = 20), # C -> Pa
wind.speed = 5, # m s-1
net.irradiance = 10) # W m-2## [1] 0.01733964 0.01733277 0.01732590 0.01731904 0.01731217 0.01730530 0.01729843
## [8] 0.01729157 0.01728470Potential evapotranspiration is in most situation proportional to the available radiant energy.
ET_ref_irrad.df <-
data.frame(irrad = (1:40) * 10,
ET.ref = ET_ref(temperature = 20, # C
water.vp = water_RH2vp(relative.humidity = 70, # RH%
temperature = 20), # C -> Pa
wind.speed = 5, # m s-1
net.irradiance = (1:40) * 10) # W m-2
)
ggplot(ET_ref_irrad.df, aes(irrad, ET.ref)) +
geom_line() +
labs(x = expression("Global radiation "*(W~m^{-2})),
y = expression("Reference evapotranspiration "*(mm~h^{-1})))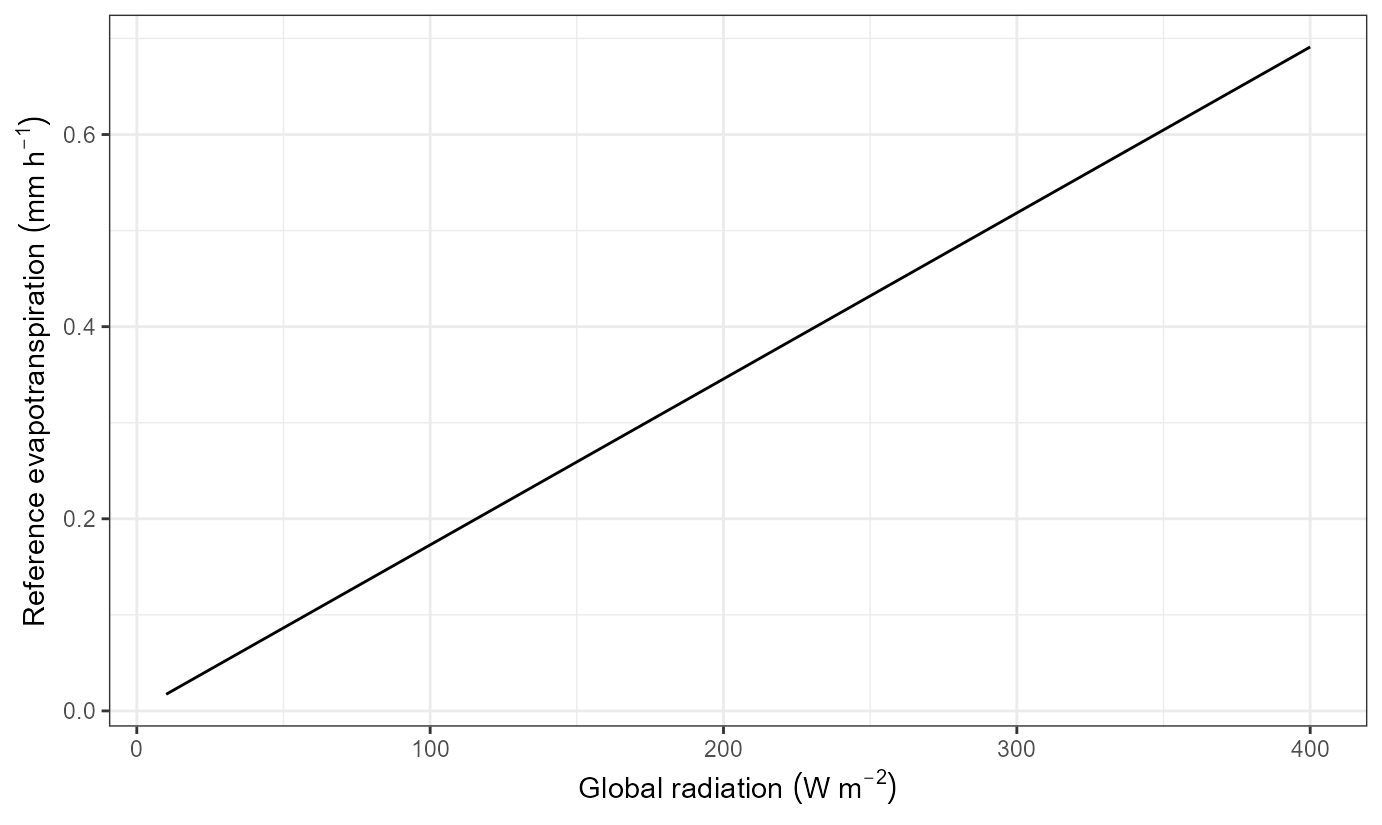
Function net_irradiance() simplifies the computation of
net irradiance, needed as input for the computation of reference
evapotranspiration.
Water vapour in air
Water vapour partial pressure in air depends on temperature and on
whether air is in equilibrium with liquid water or ice.Not considered
here, solutes in water and surface interactions also affect the
equilibrium. The examples below use the default equation for the
computation of saturated water vapour pressure. The default is Tetens’
equation from 1930. Currently supported methods are
"tetens", modified "magnus",
"wexler" and "goff.gratch".
water_vp_sat(20) # temperature in C, partial pressure in Pa## [1] 2338.023
water_vp_sat(20) * 1e-3 # temperature in C, partial pressure in kPa## [1] 2.338023
vp_sat.df <- data.frame(temperature = -20:100,
vp.sat = c(water_vp_sat(-20:-1, over.ice = TRUE),
water_vp_sat(0:100)) * 1e-3)
ggplot(vp_sat.df, aes(temperature, vp.sat)) +
geom_line() +
labs(x = "Temperature (C)", y = "Water valour pressure at saturation (kPa)")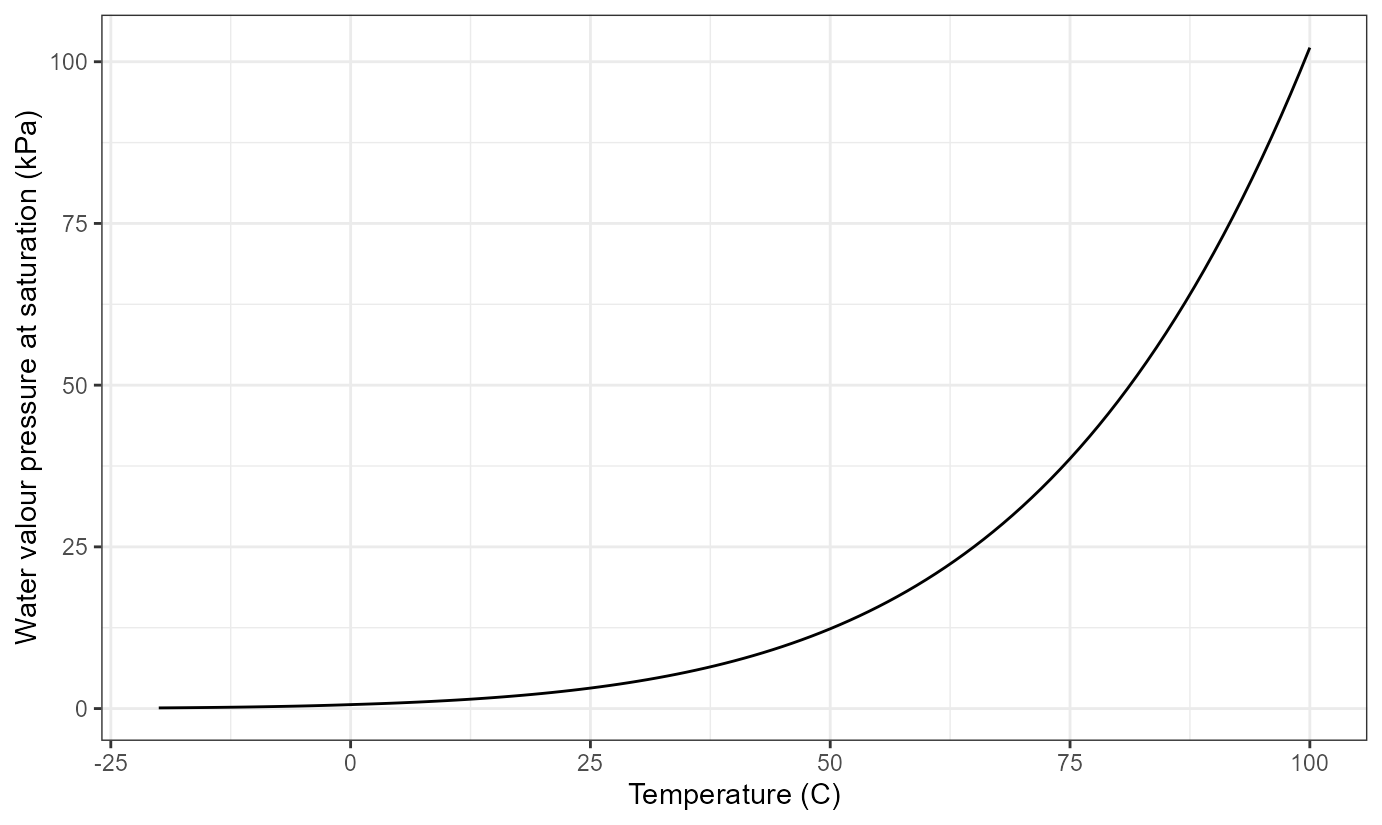
Conversion of water vapour pressure to relative humidity and vice versa is based on the curve shown in the figure above.
water_vp2RH(1000, 25) # Pa and C -> RH%## [1] 31.57191
water_vp2mvc(1000, 25) # Pa and C -> mass per volume g m-3## [1] 7.264556The reverse conversion functions are water_RH2vp(),
water_mvc2vp().
If we know the actual vapour pressure we can compute at which temperature this pressure would the saturating (RH = 100%), or dew point.
water_dp(1000) # Pa -> C ## [1] 6.973856If the vapour pressure is very low, instead of dew point we have to compute the freezing point.
water_fp(500) # Pa -> C ## [1] -2.40697Function water_vp_sat_slope() can be used to compute the
slope of the curve in the figure above as a function of air temperature,
and function psychrometric_constant() to compute the
psychrometric constant as a function of air temperature.