Custom Polynomial Models
‘ggpmisc’ 0.6.2.9001
Pedro J. Aphalo
2025-08-25
Source:vignettes/articles/poly-advanced.Rmd
poly-advanced.RmdAims of ‘ggpmisc’ and caveats
Package ‘ggpmisc’ makes it easier to add to plots created using ‘ggplot2’ annotations based on fitted models and other statistics. It does this by wrapping existing model fit and other functions. The same annotations can be produced by calling the model fit functions, extracting the desired estimates and adding them to plots. There are two advantages in wrapping these functions in an extension to package ‘ggplot2’: 1) we ensure the coupling of graphical elements and the annotations by building all elements of the plot using the same data and a consistent grammar and 2) we make it easier to annotate plots to the casual user of R, already familiar with the grammar of graphics.
To avoid confusion it is good to make clear what may seem obvious to some: if no plot is needed, then there is no reason to use this package. The values shown as annotations are not computed by ‘ggpmisc’ but instead by the usual model-fit and statistical functions from R and R packages. The same is true for model predictions, residuals, etc. that some of the functions in ‘ggpmisc’ display as lines, segments, or other graphical elements.
It is also important to remember that in most cases data analysis including exploratory and other stages should take place before annotated plots for publication are produced. Even though data analysis can benefit from combined numerical and graphical representation of the results, the use I envision for ‘ggpmisc’ is mainly for the production of plots for publication or communication. In case case, whether used for analysis or communication, it is crucial that users cite and refer both to ‘ggpmisc’ and to the underlying R and R packages when publishing plots created with functions and methods from ‘ggpmisc’.
Preliminaries
Other packages are loaded in the section they are used.
Attaching package ‘ggpmisc’ also attaches package ‘ggpp’ as it provides several of the geometries used by default in the statistics described below. Package ‘ggpp’ can be loaded and attached on its own, and has separate documentation.
As we will use text and labels on the plotting area we change the default theme to an uncluttered one.
Fitted models in stat_poly_line() and
stat_poly_eq()
Both functions are designed for flexibility while still attempting to keep their implementation and use rather straightforward.
Function stat_poly_eq() requires that the model
formula is a regular polynomial (with no missing
intermediate power terms), with the exception that the intercept can be
missing. Function stat_poly_line() has fewer
requirements for the argument passed to formula.
Both statistics: * Accept any R function or its name as argument for
method, * as long as fitted model object belongs to classes
"lm", "rlm", "lqs",
"lts" or "gls", as tested with
inherits(), and additionally models of other classes as
long as methods are available. * Their implementation tolerates some
missing methods and fields in model fit objects and their summary, i.e.,
returning NA_real_ or empty character strings
depending on the case. * The formula used to construct the equation is,
whenever possible, extracted from the fitted model object. Only
exceptionally, with this approach fails, the formula passed as argument
for formula in the call is used with a warning.
This design makes it possible to use as method existing
model fit functions that return an object of one of the classes
specifically supported, wrapper functions that call such functions, or
in some other way return an object of a known class such as
"lm" or a class with suitable methods implemented.
To showcase this, I explore the use of contributed and user defined model fit functions through examples. Several of the examples use facets or grouping to demonstrate how the models fitted depend on the data. The approach can be also useful in the absence of facets and/or groups, for example for dynamic reports or dashboards.
Two frequently use model fit functions that return model fit objects
that require special handling to extract values are supported in
‘ggpmisc’ by specific statistics: stat_ma_line() and
stat_ma_eq() for mayor axis regression with package
‘lmodel2’, and stat_quant_line(),
stat_quant_band() and stat_quant_equation()
for quantile regression with package ‘quantreg’. Their use is documented
in the User Guide and their help pages.
Existing functions
We consider cases in which fitting linear models with ordinary least squares (OLS) as criterion is unsuitable.
In the case of outliers, many methods are available, and each fit function usually also supports several variations within a class of methods. In robust regression the weight of extreme observations in the computation of the penalty function is decreased compared to OLS. The effect of such decrease can be described as weights ranging continuously between 0 and 1, either actually used in the fit algorithm or computed a posteriori by comparison to OLS. In resistant regression, some observations are ignored altogether, which is equivalent to discrete weights taking one of two values, 0 or 1. Even if these approaches work automatically, similarly as when discarding observations manually, it is important to investigate the origin of outliers.
Generalised least squares (GLS) is an extension to OLS that makes it possible to describe how the variance of the response y varies. GLS supports description of heterogeneous variance by means of variance covariates, and correlation structures.
Error in variance (EIV) methods remove the assumption that the values of the covariate x are measured/known without error. It is important here to stress that linear models (LM) do not require us to assume that there is no variation in x, only that we have observed/measured/know these values without error. To apply most of these methods, we need independently obtained information about the size of the measuring errors affecting covariates.
Not exemplified here, major axis regression (MA), is useful
when both x and y values are affected to comparable
extents by measurement errors. This is typically the case when there is
no causal direction between x and y such as in
allometric relationships between body parts of the same individual. See
stat_ma_line() and stat_ma_eq().
Quantile regression can be thought as similar to both a
regression an a box plot. It makes it possible to fit curves that divide
the observations in 2D space into quantiles, approximately preserving
this split along a fitted curve of y on x. See
stat_quant_line(), stat_quant_band() and
stat_quant_eq().
As all these methods use different penalty functions when fitting a model to observations, they yield different estimates of parameter values for the same model formula. For several of these methods the approximate solution is obtained using numeral iteration. In these cases, it is important to check whether the solution is stable with different starting points for random number generation.
Robust regression (‘MASS’)
print(citation(package = "MASS", auto = TRUE), bibtex = FALSE)
#> To cite package 'MASS' in publications use:
#>
#> Ripley B, Venables B (2025). _MASS: Support Functions and Datasets
#> for Venables and Ripley's MASS_. doi:10.32614/CRAN.package.MASS
#> <https://doi.org/10.32614/CRAN.package.MASS>, R package version
#> 7.3-65, <https://CRAN.R-project.org/package=MASS>.Package ‘MASS’ provides function rlm() for “Robust
Fitting of Linear Models”. The returned value is an "rlm"
object. Class "rlm" is derived from "lm" so
the stats work mostly as expected. However, we need to be aware that no
R^2 or P estimates are available and the
corresponding labels are empty strings.
library(MASS)
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(method = MASS::rlm) +
stat_poly_eq(method = MASS::rlm, mapping = use_label("eq", "n"),
label.x = "right") +
facet_wrap(~class, ncol = 2)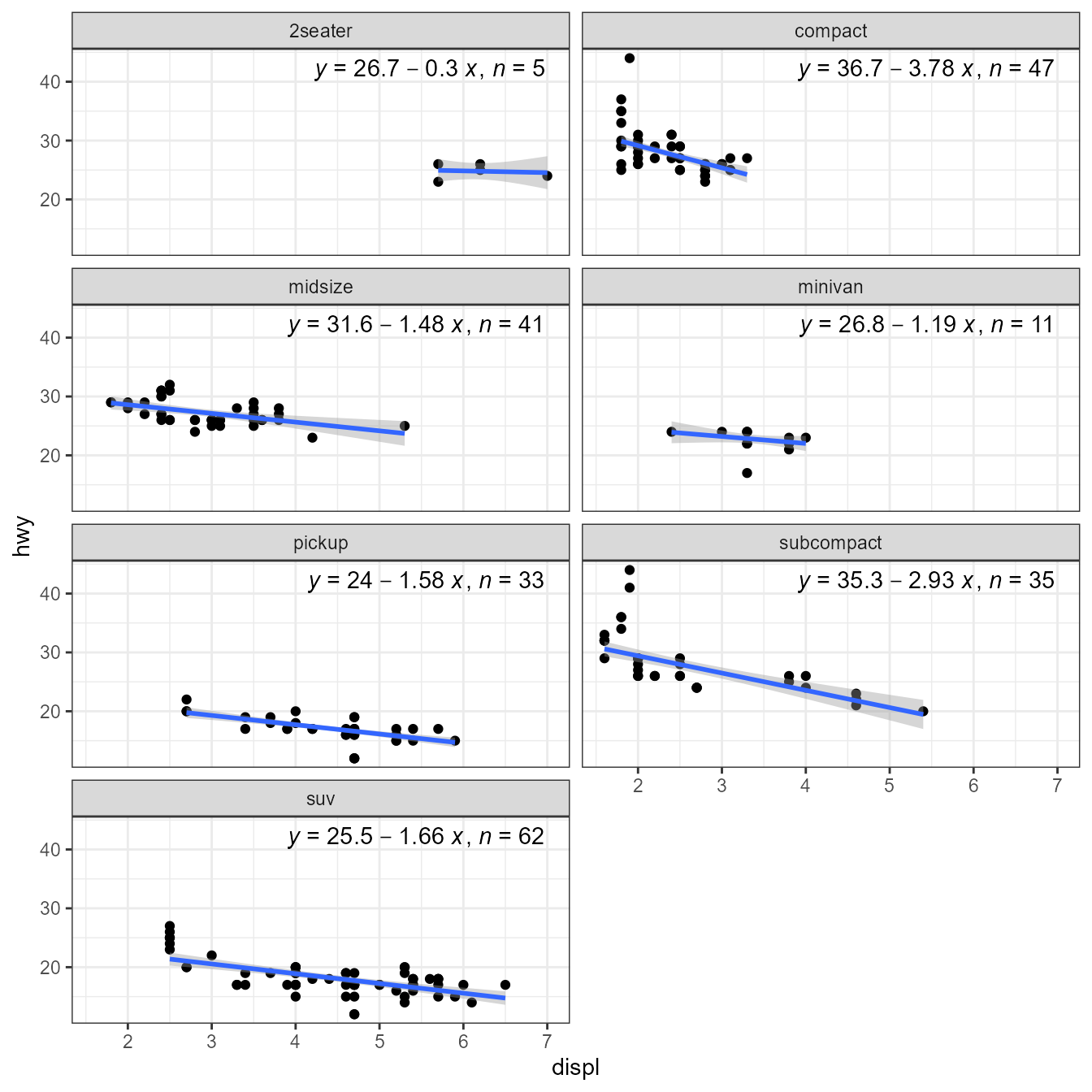
When weights are available, either supplied by the user, or computed
as part of the fit, they are returned in data. Having
weights available allows encoding them using colour. We here use a
robust regression fit with MASS::rlm().
ggplot(mpg, aes(displ, hwy)) +
stat_poly_eq(use_label("eq", "n", "method"),
label.x = "right",
method = MASS::rlm) +
stat_poly_line(method = MASS::rlm, colour = "black") +
stat_fit_deviations(method = "rlm",
mapping = aes(colour = after_stat(robustness.weights)),
show.legend = TRUE,
geom = "point") +
scale_color_gradient(low = "red", high = "blue", limits = c(0, 1)) +
theme(legend.position = "top")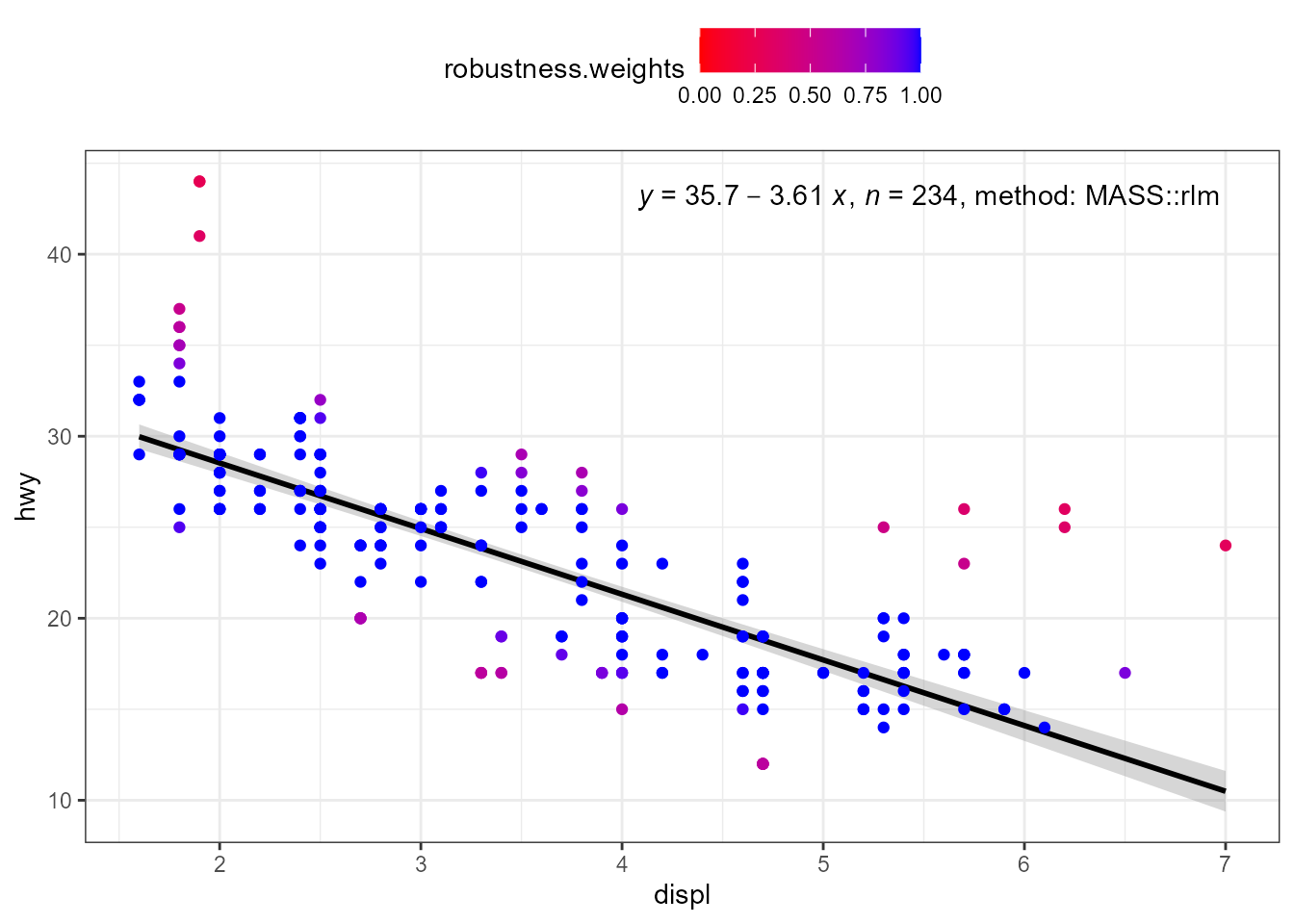
my.formula <- y ~ poly(x, 2, raw = TRUE)
ggplot(mpg, aes(displ, hwy)) +
stat_poly_eq(use_label("eq", "n", "method"),
formula = my.formula,
label.x = "right",
method = MASS::rlm) +
stat_poly_line(method = MASS::rlm,
formula = my.formula,
colour = "black") +
stat_fit_deviations(mapping = aes(colour = after_stat(robustness.weights)),
method = "rlm",
formula = my.formula,
show.legend = TRUE,
geom = "point") +
scale_color_gradient(low = "red", high = "blue", limits = c(0, 1)) +
theme(legend.position = "top")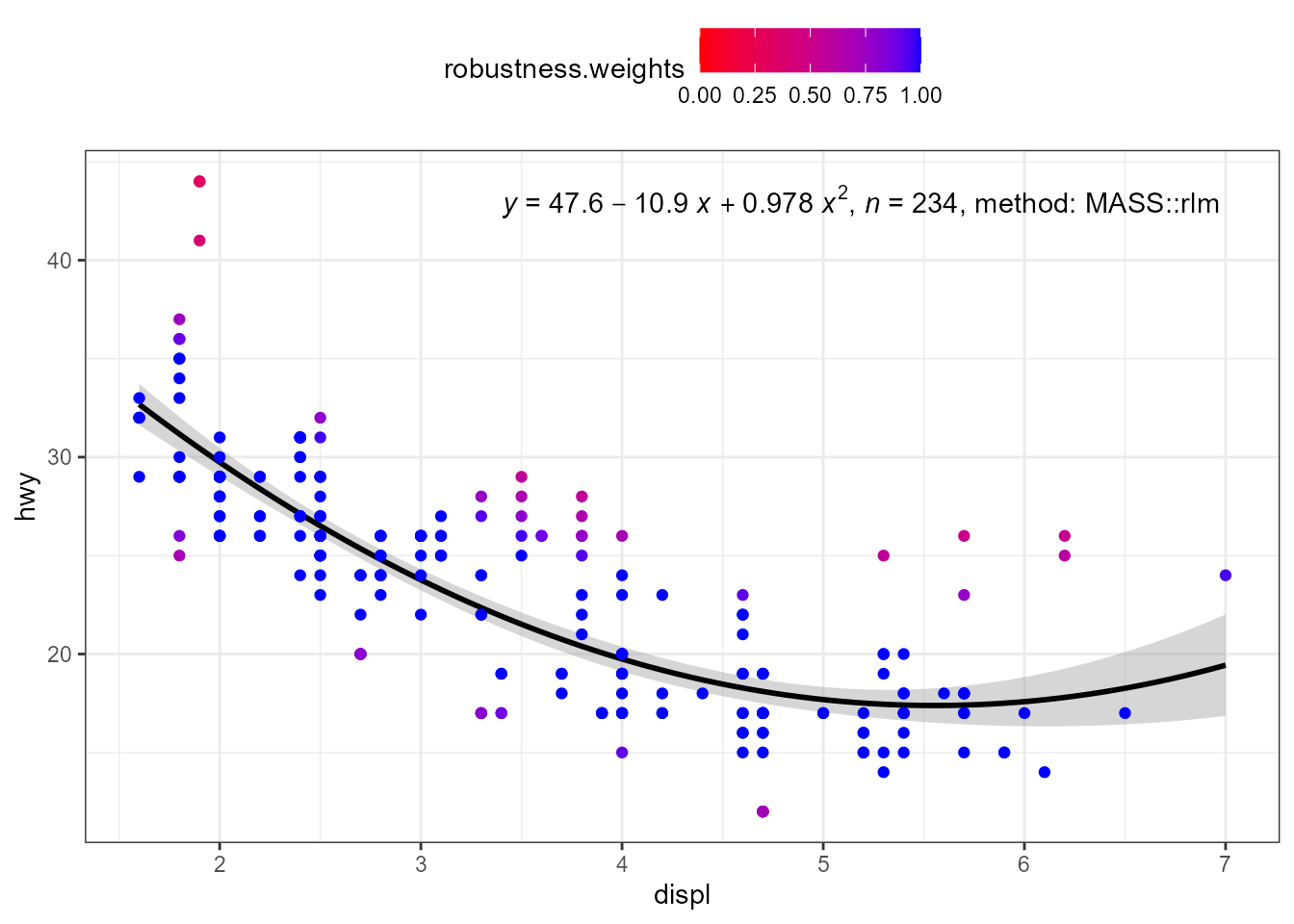
Robust regression (‘robustbase’)
print(citation(package = "robustbase", auto = TRUE), bibtex = FALSE)
#> To cite package 'robustbase' in publications use:
#>
#> Maechler M, Todorov V, Ruckstuhl A, Salibian-Barrera M, Koller M,
#> Conceicao EL (2024). _robustbase: Basic Robust Statistics_.
#> doi:10.32614/CRAN.package.robustbase
#> <https://doi.org/10.32614/CRAN.package.robustbase>, R package version
#> 0.99-4-1, <https://CRAN.R-project.org/package=robustbase>.Package ‘robustbase’ provides function lmrob() for
“MM-type Estimators for Linear Regression”. The returned value is an
"lmrob" object. Class "lmrob" is derived from
"lm" so the stats work mostly as expected. However, we need
to be aware that no R^2 or P estimates are available and the
corresponding labels are empty strings.
library(robustbase)
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(method = robustbase::lmrob) +
stat_poly_eq(method = robustbase::lmrob, mapping = use_label("eq", "R2"),
label.x = "right") +
theme(legend.position = "bottom") +
facet_wrap(~class, ncol = 2)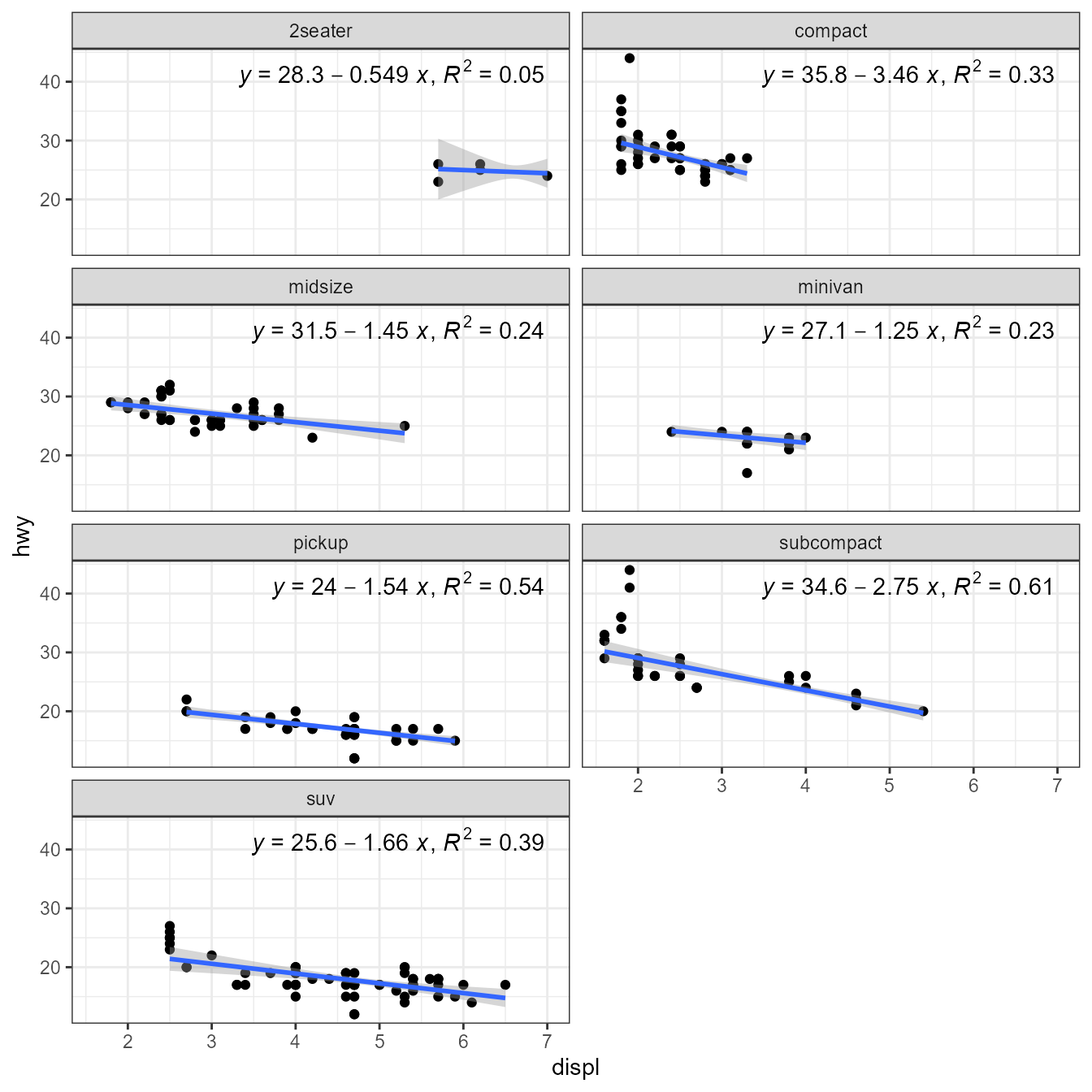
When weights are available, either supplied by the user, or computed
as part of the fit, they are returned in data. Having
weights available allows encoding them using colour. We here use a
robust regression fit with MASS::rlm().
ggplot(mpg, aes(displ, hwy)) +
stat_poly_eq(use_label("eq", "R2", "method"),
label.x = "right",
method = robustbase::lmrob) +
stat_poly_line(method = robustbase::lmrob, colour = "black") +
stat_fit_deviations(method = robustbase::lmrob,
mapping = aes(colour = after_stat(robustness.weights)),
show.legend = TRUE,
geom = "point") +
scale_color_gradient(name = "Robustness weights",
low = "red", high = "blue", limits = c(0, 1)) +
theme(legend.position = "top")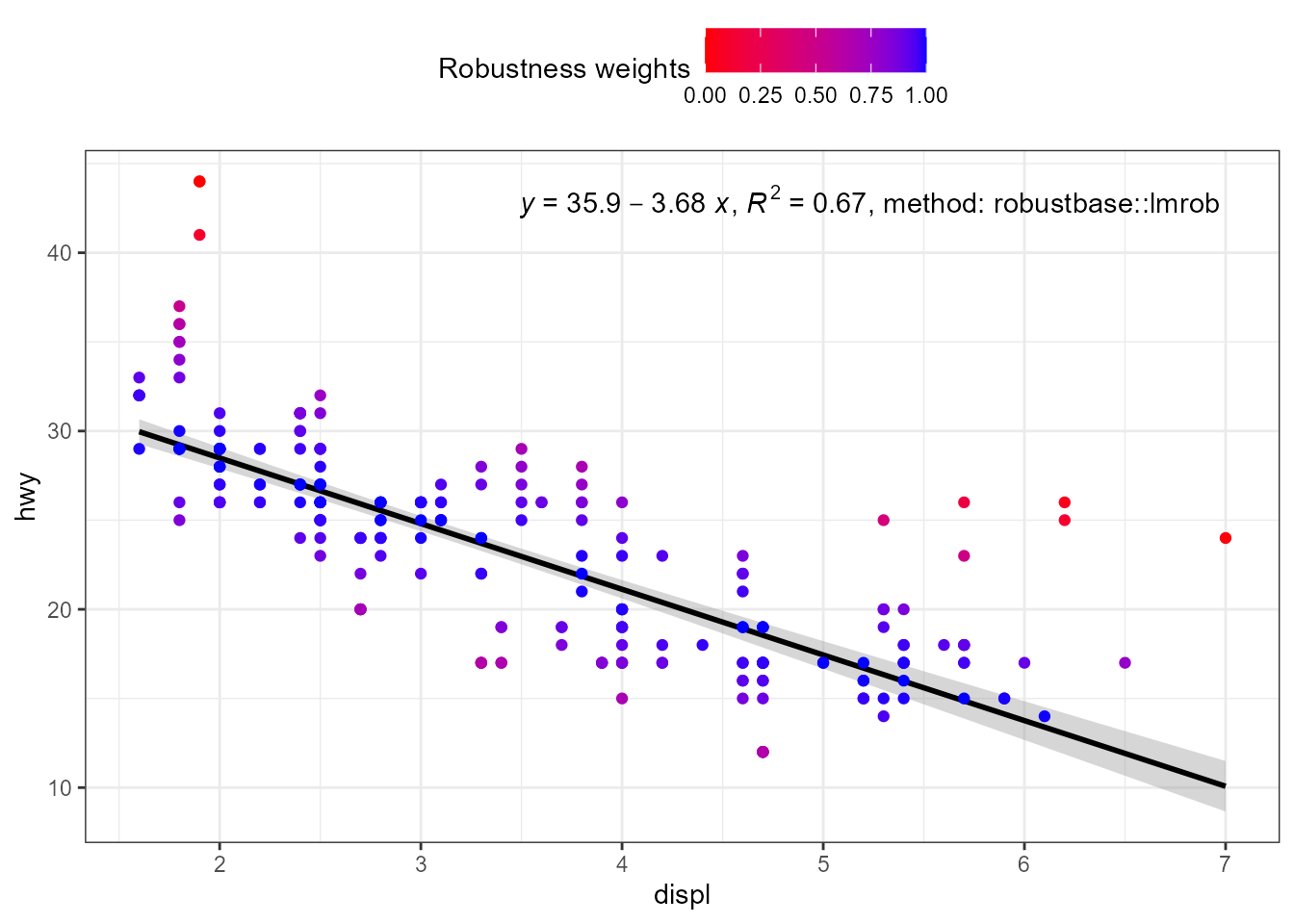
my.formula <- y ~ poly(x, 2, raw = TRUE)
ggplot(mpg, aes(displ, hwy)) +
stat_poly_eq(use_label("eq", "R2", "method"),
formula = my.formula,
label.x = "right",
method = robustbase::lmrob) +
stat_poly_line(method = robustbase::lmrob,
formula = my.formula,
colour = "black") +
stat_fit_deviations(method = robustbase::lmrob,
mapping = aes(colour = after_stat(robustness.weights)),
formula = my.formula,
show.legend = TRUE,
geom = "point") +
scale_color_gradient(name = "Robustness weights",
low = "red", high = "blue", limits = c(0, 1)) +
theme(legend.position = "top")
Resistant regression (‘MASS’)
print(citation(package = "MASS", auto = TRUE), bibtex = FALSE)
#> To cite package 'MASS' in publications use:
#>
#> Ripley B, Venables B (2025). _MASS: Support Functions and Datasets
#> for Venables and Ripley's MASS_. doi:10.32614/CRAN.package.MASS
#> <https://doi.org/10.32614/CRAN.package.MASS>, R package version
#> 7.3-65, <https://CRAN.R-project.org/package=MASS>.Package ‘MASS’ provides function lqs() for “Resistant
Regression”. The returned value is an "lqs" object. Class
"rlm" is not derived from "lm" but the
structure is similar. However, we need to be aware that no R^2 or P
estimates are available and the corresponding labels are empty
strings.
library(MASS)
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(method = MASS::lqs, se = FALSE) +
stat_poly_eq(method = MASS::lqs, mapping = use_label("eq", "n"),
label.x = "right") +
theme(legend.position = "bottom") +
facet_wrap(~class, ncol = 2)
Weights are currently not available for MASS::lqs() and
NA vectors are returned instead. To highlight the LTS
weights, rosbustbase::ltsReg() can be used as shown in the
next section.
ggplot(mpg, aes(displ, hwy)) +
stat_poly_eq(use_label("eq", "n", "method"),
label.x = "right",
method = MASS::lqs) +
stat_poly_line(method = "lqs:lms", colour = "black") +
stat_fit_deviations(method = MASS::lqs,
mapping =
aes(colour = factor(after_stat(robustness.weights))),
show.legend = TRUE,
geom = "point") +
scale_color_manual(name = "LTS weights",
values = c("0" = "red", "1" = "black")) +
theme(legend.position = "top")
my.formula <- y ~ poly(x, 2, raw = TRUE)
ggplot(mpg, aes(displ, hwy)) +
stat_poly_eq(use_label("eq", "n", "method"),
formula = my.formula,
label.x = "right",
method = MASS::lqs) +
stat_poly_line(method = "lqs:lms",
formula = my.formula,
colour = "black") +
stat_fit_deviations(mapping =
aes(colour = factor(after_stat(robustness.weights))),
method = MASS::lqs,
formula = my.formula,
show.legend = TRUE,
geom = "point") +
scale_color_manual(name = "LTS weights",
values = c("0" = "red", "1" = "black")) +
theme(legend.position = "top")
Resistant regression (‘robustbase’)
print(citation(package = "robustbase", auto = TRUE), bibtex = FALSE)
#> To cite package 'robustbase' in publications use:
#>
#> Maechler M, Todorov V, Ruckstuhl A, Salibian-Barrera M, Koller M,
#> Conceicao EL (2024). _robustbase: Basic Robust Statistics_.
#> doi:10.32614/CRAN.package.robustbase
#> <https://doi.org/10.32614/CRAN.package.robustbase>, R package version
#> 0.99-4-1, <https://CRAN.R-project.org/package=robustbase>.Package ‘robustbase’ provides function ltsReg() for
“least trimmed squares” regression. The returned value is an
"lts" object. The usual accessors functions are available
for Class "lts".
library(robustbase)
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(method = robustbase::ltsReg, se = FALSE) +
stat_poly_eq(method = robustbase::ltsReg, mapping = use_label("eq", "n"),
label.x = "right") +
theme(legend.position = "bottom") +
facet_wrap(~class, ncol = 2)
#> Fitted line plotted
#> Fitted line plotted
#> Fitted line plotted
#> Fitted line plotted
#> Fitted line plotted
#> Fitted line plotted
#> Fitted line plotted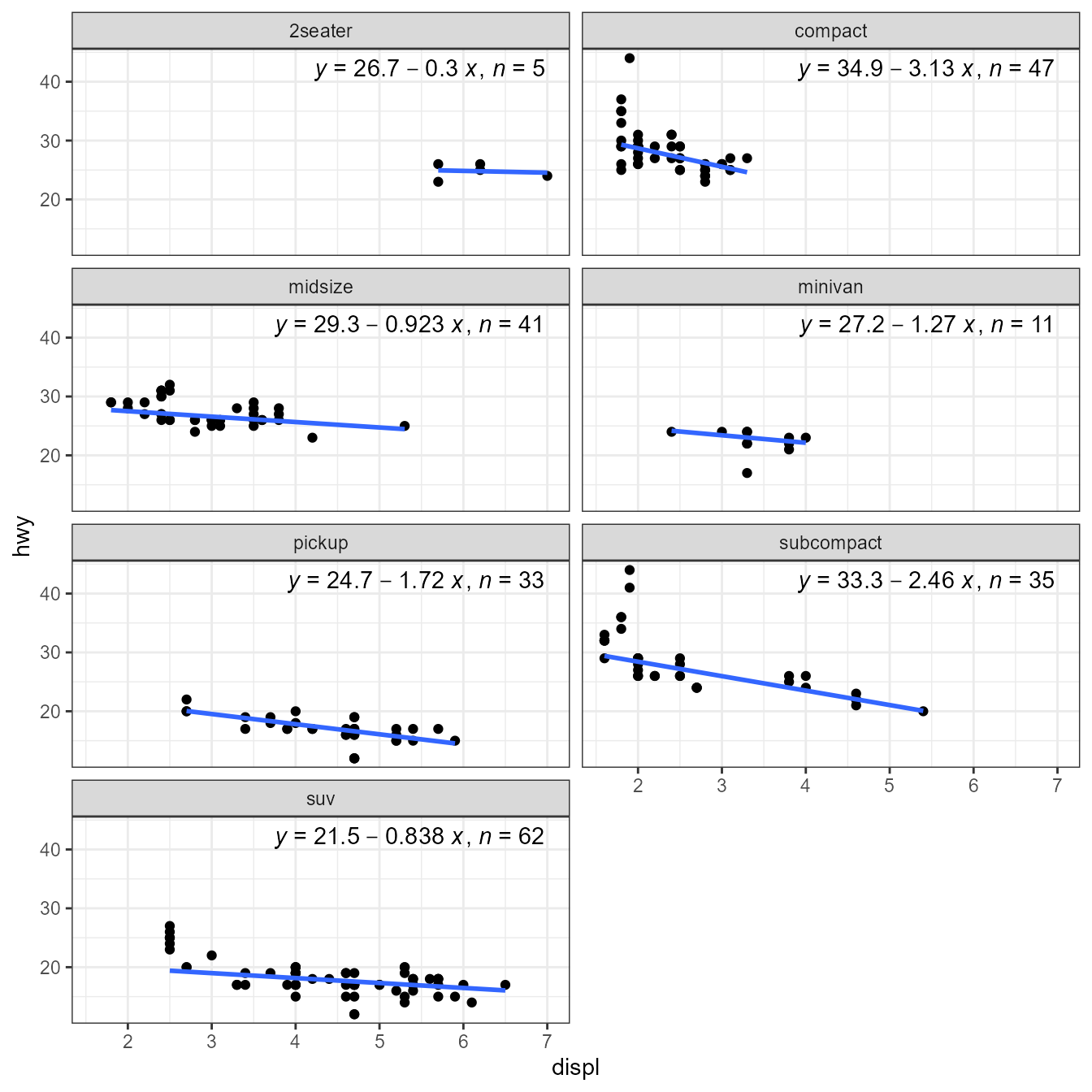
If no predict() method is found for a model fit
object, stat_poly_line() searches for method
fitted(), which is nearly always available. This is how the
"lts" objects returned by robustbase::ltsReg()
are by default supported.
For a linear regression, unless extrapolation is attempted this makes
little, if any, difference to the line but no confidence band is
displayed. With higher degree polynomials and sparse data this approach
can result in a curve that is not smooth. It is possible for users to
define the missing specialization for the predict() method.
Predicting the fitted line using coefficients() and the
known formula is straightforward, while estimating a
prediction confidence band can be more difficult.
ggplot(mpg, aes(displ, hwy)) +
stat_poly_eq(use_label("eq", "R2", "method"),
label.x = "right",
method = robustbase::ltsReg) +
stat_poly_line(method = robustbase::ltsReg, colour = "black") +
stat_fit_deviations(mapping = aes(colour = factor(after_stat(robustness.weights))),
geom = "point",
method = robustbase::ltsReg,
show.legend = TRUE) +
scale_color_manual(name = "LTS weights",
values = c("0" = "red", "1" = "blue")) +
theme(legend.position = "top")
#> Fitted line plotted
my.formula <- y ~ poly(x, 2, raw = TRUE)
ggplot(mpg, aes(displ, hwy)) +
stat_poly_eq(use_label("eq", "R2", "method"),
label.x = "right",
formula = my.formula,
method = robustbase::ltsReg) +
stat_poly_line(method = robustbase::ltsReg,
formula = my.formula,
colour = "black") +
stat_fit_deviations(mapping = aes(colour = factor(after_stat(robustness.weights))),
formula = my.formula,
geom = "point",
method = robustbase::ltsReg,
show.legend = TRUE) +
scale_color_manual(name = "LTS weights",
values = c("0" = "red", "1" = "blue")) +
theme(legend.position = "top")
#> Fitted line plotted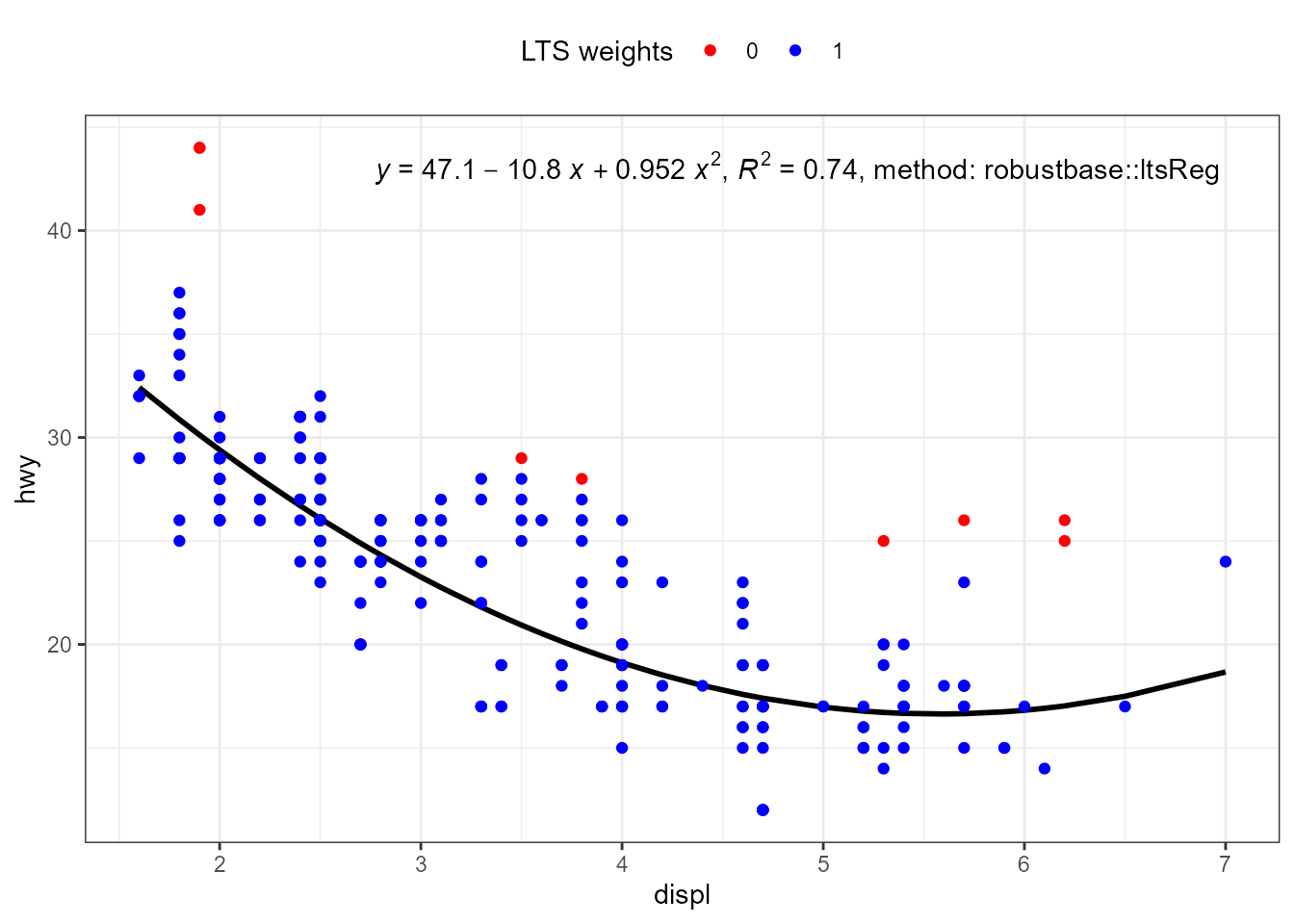
Generalized Least Squares (‘nlme’)
print(citation(package = "nlme", auto = TRUE), bibtex = FALSE)
#> To cite package 'nlme' in publications use:
#>
#> Pinheiro J, Bates D, R Core Team (2025). _nlme: Linear and Nonlinear
#> Mixed Effects Models_. doi:10.32614/CRAN.package.nlme
#> <https://doi.org/10.32614/CRAN.package.nlme>, R package version
#> 3.1-168, <https://CRAN.R-project.org/package=nlme>.In ‘ggpmisc’ (>= 0.6.2) function gls() from package
‘nlme’ is supported natively by functions stat_poly_line()
and stat_poly_eq(). In this example, using a variance
covariate, the computations do not converge with the data in one of the
plot panels.
library(nlme)
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(method = gls,
method.args = list(weights = varPower()),
se = FALSE) +
stat_poly_eq(method = gls,
method.args = list(weights = varPower()),
mapping = use_label("eq"),
label.x = "right") +
theme(legend.position = "bottom") +
facet_wrap(~class, ncol = 2)
#> Warning: Computation failed in `stat_poly_line()`.
#> Caused by error:
#> ! maximum number of iterations reached without convergence
#> Warning: Computation failed in `stat_poly_eq()`.
#> Caused by error:
#> ! maximum number of iterations reached without convergence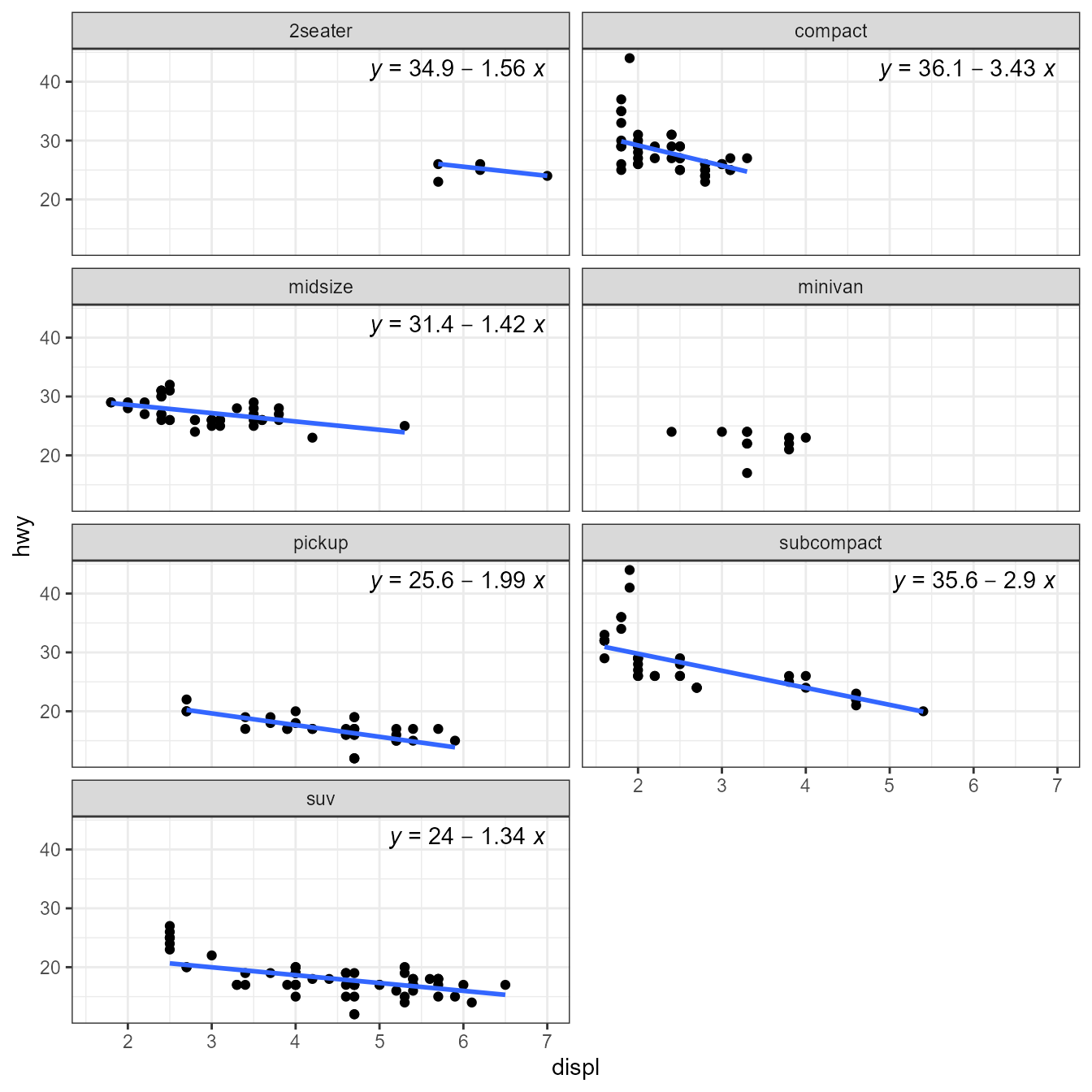
Linear Splines (‘lspline’)
print(citation(package = "lspline", auto = TRUE), bibtex = FALSE)
#> To cite package 'lspline' in publications use:
#>
#> Bojanowski M (2017). _lspline: Linear Splines with Convenient
#> Parametrisations_. doi:10.32614/CRAN.package.lspline
#> <https://doi.org/10.32614/CRAN.package.lspline>, R package version
#> 1.0-0, <https://CRAN.R-project.org/package=lspline>.Package ‘lspline’ provides functions that can be used to fit linear
splines with function lm(). These functions are called from
the model formula, and do not fit the change points where the knots are
located. These functions, lspline(),
qlspline() amd elspline() can be used directly
in the model formula passed to stat_poly_line(). They can
be used also with stat_poly_eq() but the equation label
returned is incorrect, with the terms for the different segments
displayed as the terms for the powers of a polynomial. Thus, it is
necessary to construct in the call to aes() the equations
for the different segments. The other labels are correctly
generated.
library(lspline) # attachment needed for methods to be available
cp <- 4.1 # a guess
my.formula <- y ~ lspline(x, knots = cp)
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_eq(aes(label =
paste("\"L : \"*y~`=`~", round(after_stat(b_0), 2),
round(after_stat(b_1), 2), "~x",
"*\"; R: \"*y~`=`~",
round(after_stat(b_0) + cp * after_stat(b_1), 2),
round(after_stat(b_2), 2), "~x",
sep = "")),
parse = TRUE, output.type = "numeric",
label.x = "right",
formula = my.formula,
method = "lm") +
stat_poly_eq(use_label("R2", "P", "AIC"),
label.x = "right",
label.y = 0.87,
formula = my.formula,
method = "lm") +
stat_poly_line(method = "lm",
formula = my.formula)
It is posisble to use rlm() instead of
lm().
cp <- 4.1
my.formula <- y ~ lspline(x, knots = cp)
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_eq(aes(label =
paste("\"L : \"*y~`=`~", round(after_stat(b_0), 2),
round(after_stat(b_1), 2), "~x",
"*\"; R: \"*y~`=`~",
round(after_stat(b_0) + cp * after_stat(b_1), 2),
round(after_stat(b_2), 2), "~x",
sep = "")),
parse = TRUE, output.type = "numeric",
label.x = "right",
formula = my.formula,
method = "rlm") +
stat_poly_eq(use_label("AIC"),
label.x = "right",
label.y = 0.87,
formula = my.formula,
method = "rlm") +
stat_poly_line(method = "rlm",
formula = my.formula)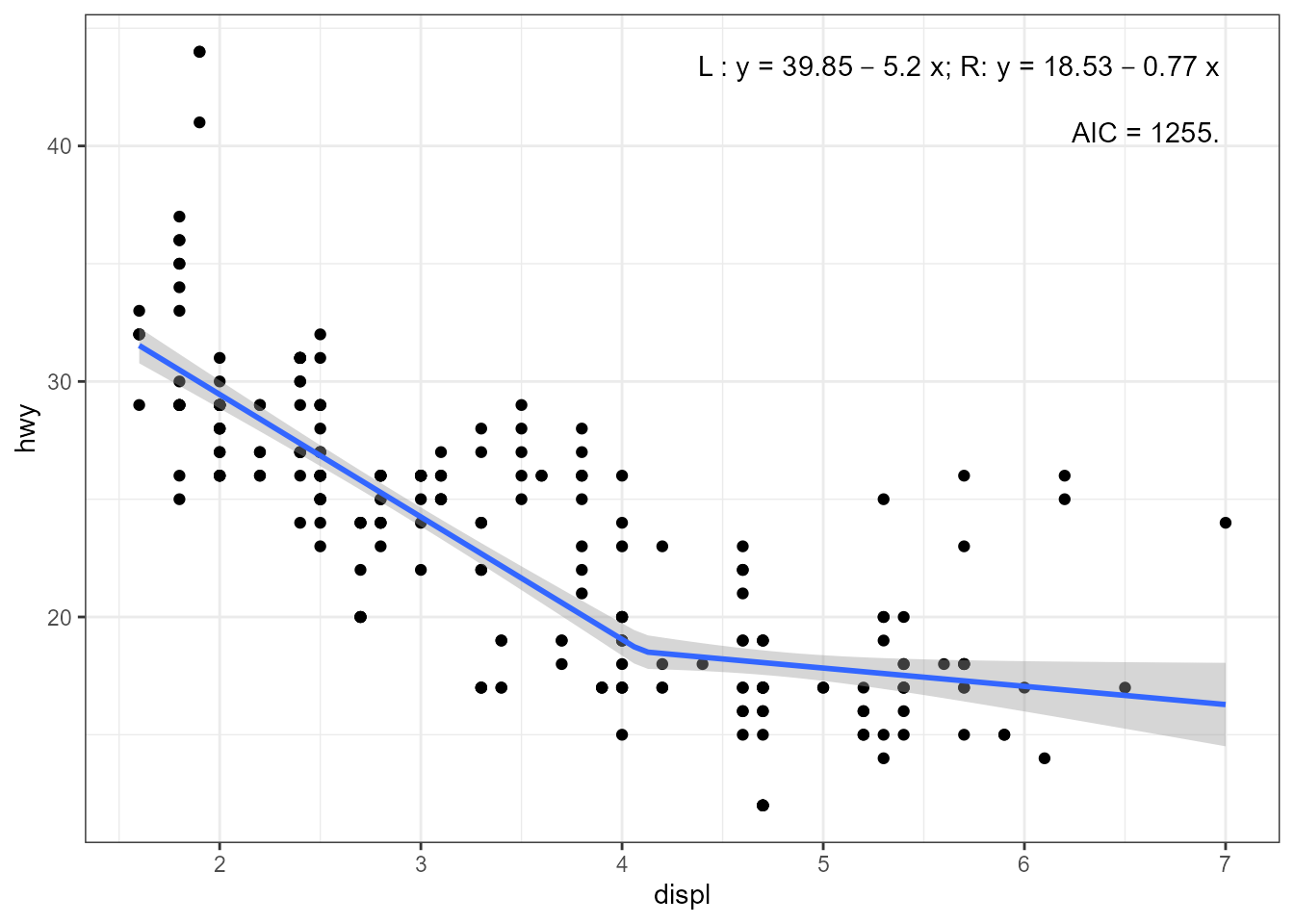
Linear Splines (‘segmented’)
Package ‘segmented’ has a design that makes it easy to use. The
fitted model used has a structure consistent with that returned by
lm(). Any differences are smoothed by query/extract
functions that are consistent with those for "lm" objects.
As segmented linear models are not polynomials, no eq.label
is automatically generated. Another difference is that the location of
change points is estimated and returned. Starting from ‘ggpmisc’ (>=
0.6.3) this information is returned by stat_poly_eq() and
can be used to in user-assembled labels as shown in the examples
below.
print(citation(package = "segmented", auto = TRUE), bibtex = FALSE)
#> To cite package 'segmented' in publications use:
#>
#> Muggeo VMR (2025). _segmented: Regression Models with Break-Points /
#> Change-Points Estimation (with Possibly Random Effects)_.
#> doi:10.32614/CRAN.package.segmented
#> <https://doi.org/10.32614/CRAN.package.segmented>, R package version
#> 2.1-4, <https://CRAN.R-project.org/package=segmented>.Function segreg() makes it possible to fit LM and GLM
models that are segmented. Differently to ‘lspline’, the location of the
change points or spline knots is estimated during model fitting in
addition to estimating segment slopes and intercept. As ‘lspline’ it
uses a model formula to set the model including control of the
segmentation through seg(). Differently to
lspline(), segreg() is a model fit function
that returns a fitted model object with additional information on change
points and slopes.
The model formula = y ~ seg(x, npsi = 1) requests a fit
with a single change point, which being the default is equivalent to
formula = y ~ seg(x).
library(segmented)
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_eq(aes(label =
paste("x[cp]~`=`~",
round(after_stat(knots)[[1]][1], 2),
" %+-% ",
round(after_stat(knots.se)[[1]][1], 2),
"*\"; L: \"*y~`=`~",
round(after_stat(b_0), 2), # "+",
round(after_stat(b_1), 2), "~x",
"*\"; R: \"*y~`=`~",
round(after_stat(b_0) +
after_stat(knots)[[1]][1] *
(after_stat(b_1) - after_stat(b_2)),
2),
"+",
round(after_stat(b_2), 2), "~x",
sep = "")),
parse = TRUE, output.type = "numeric",
label.x = "right",
formula = y ~ seg(x, npsi = 1),
method = segreg) +
stat_poly_eq(use_label("R2", "P", "AIC"),
label.x = "right",
label.y = 0.87,
formula = y ~ seg(x, npsi = 1),
method = segreg) +
stat_poly_line(method = segreg,
formula = y ~ seg(x, npsi = 1))
In the next example the slope of the second segment is fixed at zero
to keep it horizontal using
formula = y ~ seg(x, npsi = 1, est = c(1, 0)) where 1
indicates a fitted slope and 0 a slope fixed at this value. Because of
how the parameters are returned, the code to assemble the equation needs
to be rewritten.
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_eq(aes(label =
paste("x[cp]~`=`~",
round(after_stat(knots)[[1]][1], 2),
" %+-% ",
round(after_stat(knots.se)[[1]][1], 2),
"*\"; L: \"*y~`=`~",
round(after_stat(b_1), 2), # "+",
round(after_stat(b_2), 2), "~x",
"*\"; R: \"*y~`=`~",
round(after_stat(b_1) +
after_stat(knots)[[1]][1] *
after_stat(b_2),
2),
sep = "")),
parse = TRUE, output.type = "numeric",
label.x = "right",
formula = y ~ seg(x, npsi = 1, est = c(1, 0)),
method = segreg) +
stat_poly_eq(use_label("R2", "P", "AIC"),
label.x = "right",
label.y = 0.87,
formula = y ~ seg(x, npsi = 1, est = c(1, 0)),
method = segreg) +
stat_poly_line(method = segreg,
formula = y ~ seg(x, npsi = 1, est = c(1, 0)))
User defined functions
As mentioned above, layer functions stat_poly_line() and
stat_poly_eq() support the use of several different model
fit functions, as long as the estimates and predictions can be
extracted. In the case of stat_poly_eq(), the model formula
embedded in this object must be a polynomial. The variables mapped to
x and y aesthetics must be continuous numeric, times
or dates. Models are fitted separately to each group and plot panel,
similarly as by ggplot2::stat_smooth(). ‘ggpmisc’ provides
additional flexibility by delaying some decisions until after the models
have been fit to the observations.
stat_poly_line() and stat_poly_eq()
adjust their behaviour based on the class of the model object returned
by the method, not the name of the method passed in the call as
argument. Thus, the class of the model fit object returned can
vary in response to data, and thus also be different for different
panels or groups in the same plot.
stat_poly_eq() builds the fitted model equation
based on the model formula extracted from the model fit object, which
can differ from that passed as argument to formula when
calling the statistic. Thus, the model formula returned by the
function passed as argument for method vary by group and/or
panel.As the examples below demonstrate, this approach can be very
useful. In addition, NA can be used to signal to
stat_poly_line() and stat_poly_eq() that no
model has been fit for a group or panel.
Below I use lm() and "lm" model fit objects
in most examples, but the same approaches can be applied to objects of
other classes, including "rlm", "lmrob",
’“lqs”,“lts”,“gls”`.
Fit or not
In the first example we fit a model only if a minimum number of
distinct x values are present in data. We define a
function that instead of fitting the model, returns NA when
the condition is not fulfilled. Here "x" is the aesthetic,
and has to be replaced by "y" depending on
orientation.
fit_or_not <- function(formula, data, ..., orientation = "x") {
if (length(unique(data[[orientation]])) > 5) {
lm(formula = formula, data = data, ...)
} else {
NA_real_
}
}Instead of using stats::lm() as method, we pass our
wrapper function fit_or_not() as the method. As the
function returns either an "lm" object from the wrapped
call to lm() or NA, the call to the statistics
can make use of all other features as needed.
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(method = "fit_or_not") +
stat_poly_eq(method = fit_or_not,
mapping = use_label("eq", "R2"),
label.x = "right") +
stat_panel_counts(label.x = "left", label.y = "bottom") +
theme(legend.position = "bottom") +
facet_wrap(~class, ncol = 2)
Degree of polynomial
Not fitting a model, is a drastic solution. An alternative that we
implement next, is to plot the mean when the slope of the linear
regression is not significantly different from zero. In the example
below instead of using stats::lm() as method, we define a
different wrapper function that tests for the significance of the slope
in linear regression, and if not significant, fits the mean instead.
_This works because the model formula is extracted from the fitted model
rather than using the argument passed by the user in the call to the
statistics.
Fitting different models to different panels is supported.
User-defined method functions are required to return an object that
inherits from class "lm". The function is applied per group
and panel, and the model formula fitted can differ among
them, as it is retrieved from this object to construct the equation
label.
In the example below instead of using stats::lm() as
method, we define a wrapper function that tests for the significance of
the slope in linear regression, and if not significant, fits the mean
instead.
poly_or_mean <- function(formula, data, ...) {
fm <- lm(formula = formula, data = data, ...)
if (anova(fm)[["Pr(>F)"]][1] > 0.1) {
lm(formula = y ~ 1, data = data, ...)
} else {
fm
}
}We then use our function poly_or_mean() as the
method.
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(method = "poly_or_mean") +
stat_poly_eq(method = poly_or_mean,
mapping = use_label("eq", "R2"),
label.x = "right") +
theme(legend.position = "bottom") +
facet_wrap(~class, ncol = 2)
ggplot(mpg, aes(displ, hwy, color = class)) +
geom_point() +
stat_poly_line(method = "poly_or_mean") +
stat_poly_eq(method = poly_or_mean,
mapping = use_label("eq"),
label.x = "right") +
theme(legend.position = "top")
A different approach to selecting the degree of a polynomial is to
use stepwise selection based on AIC. In this case the
formula passed as argument is the “upper” degree of the
polynomial. All lower degree polynomials are fitted and the one with
lowest AIC used.
best_poly_lm <- function(formula, data, ...) {
poly.term <- as.character(formula)[3]
degree <- as.numeric(gsub("poly[(]x, |, raw = TRUE|[)]", "", poly.term))
fms <- list()
AICs <- numeric(degree)
for (d in 1:degree) {
# we need to define the formula with the value of degree replaced
working.formula <- as.formula(bquote(y ~ poly(x, degree = .(d), raw = TRUE)))
fms[[d]] <- lm(formula = working.formula, data = data, ...)
AICs[d] <- AIC(fms[[d]])
}
fms[[which.min(AICs)[1]]] # if there is a tie, we take the simplest
}We then use our function best_poly_lm() as the
method.
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(formula = y ~ poly(x, 3, raw = TRUE), method = "best_poly_lm") +
stat_poly_eq(formula = y ~ poly(x, 3, raw = TRUE), method = "best_poly_lm",
mapping = use_label("eq", "AIC"),
size = 2.8,
label.x = "right") +
expand_limits(y = c(0, 65)) +
facet_wrap(~class, ncol = 2)
ggplot(mpg, aes(displ, hwy, color = class)) +
geom_point() +
stat_poly_line(formula = y ~ poly(x, 3, raw = TRUE), method = "best_poly_lm") +
stat_poly_eq(formula = y ~ poly(x, 3, raw = TRUE), method = "best_poly_lm",
mapping = use_label("eq", "AIC"),
label.x = "right") +
expand_limits(y = c(0, 65)) +
theme(legend.position = "top")
Functions that re-fit a fitted model
The examples in this section are for package ‘segmented’, however, a similar approach can be useful with any model fitting that involves calls to more than one function in sequence, such as computing starting values for a numerical method, or modifying the model fit object.
Segmented (‘segmented’)
Package ‘segmented’ implements methods for fitting models with change points. The location of the change points themselves are fitted with estimates and their standard deviations computed.
print(citation(package = "segmented", auto = TRUE), bibtex = FALSE)
#> To cite package 'segmented' in publications use:
#>
#> Muggeo VMR (2025). _segmented: Regression Models with Break-Points /
#> Change-Points Estimation (with Possibly Random Effects)_.
#> doi:10.32614/CRAN.package.segmented
#> <https://doi.org/10.32614/CRAN.package.segmented>, R package version
#> 2.1-4, <https://CRAN.R-project.org/package=segmented>.The code here, is equivalent to that shown above based on model-fit
function segreg() also from package ‘segmented’. The
difference is that when using segmented() the fitting is
done in two steps. In this case there is no need to use this approach,
but it can be useful when segmentation is to be applied only to some
plot panels or applied conditionally in single panel plots. Another use
is when fitting segmented linear regressions based on model-fit
functions other than lm() or glm(). However,
in this second case, some of the necessary model-fit query functions can
be unavailable and may need to be defined by the user. There are also
model fit methods that do not compute or provide the estimates required
by the segmentation computations.
Package ‘segmented’ provides several specializations of method
segmented(). These methods are dispathed according the
model fit object passed to parameter obj. As this package
provides all the expected query functions for the object
segmented() methods return, their use is not too difficult.
It is possible to write a wrapper function to pass as argument to
stat_poly_line() and stat_poly_eq() and in
addition, if used, construct the fitted equation labels within a call to
aes(). This function, that I named lm2segmented.lm, calls
first lm() and then calls segmented() with the
fitted model as argument. It accepts additional arguments that make it
possible to control the number and initial values of the knots. As in
the case of other model fit functions, models with multiple explanatory
variables are rarely used with ‘ggplot2’ stats.
library(segmented)
lm2segmented.lm <-
function(formula,
data,
seg.Z = ~ x, # explanatory variable used for segmentation
psi = median(data$x), # starting value(s) for knot(s)
npsi = 1, # number of knots if psi is not given
fixed.psi = NULL, # breakpoint not to be modified by fitting
control = segmented::seg.control(),
...) {
obj <- lm(formula = formula, data = data, ...)
segmented(obj = obj,
seg.Z = seg.Z,
psi = psi,
npsi = npsi,
fixed.psi = fixed.psi,
control = control,
model = TRUE,
keep.class = FALSE)
}
# using defaults, one breakpoint
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(method = lm2segmented.lm)
# requesting two breakpoints with starting values
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(method = lm2segmented.lm,
method.args = list(psi = c(3, 5)))
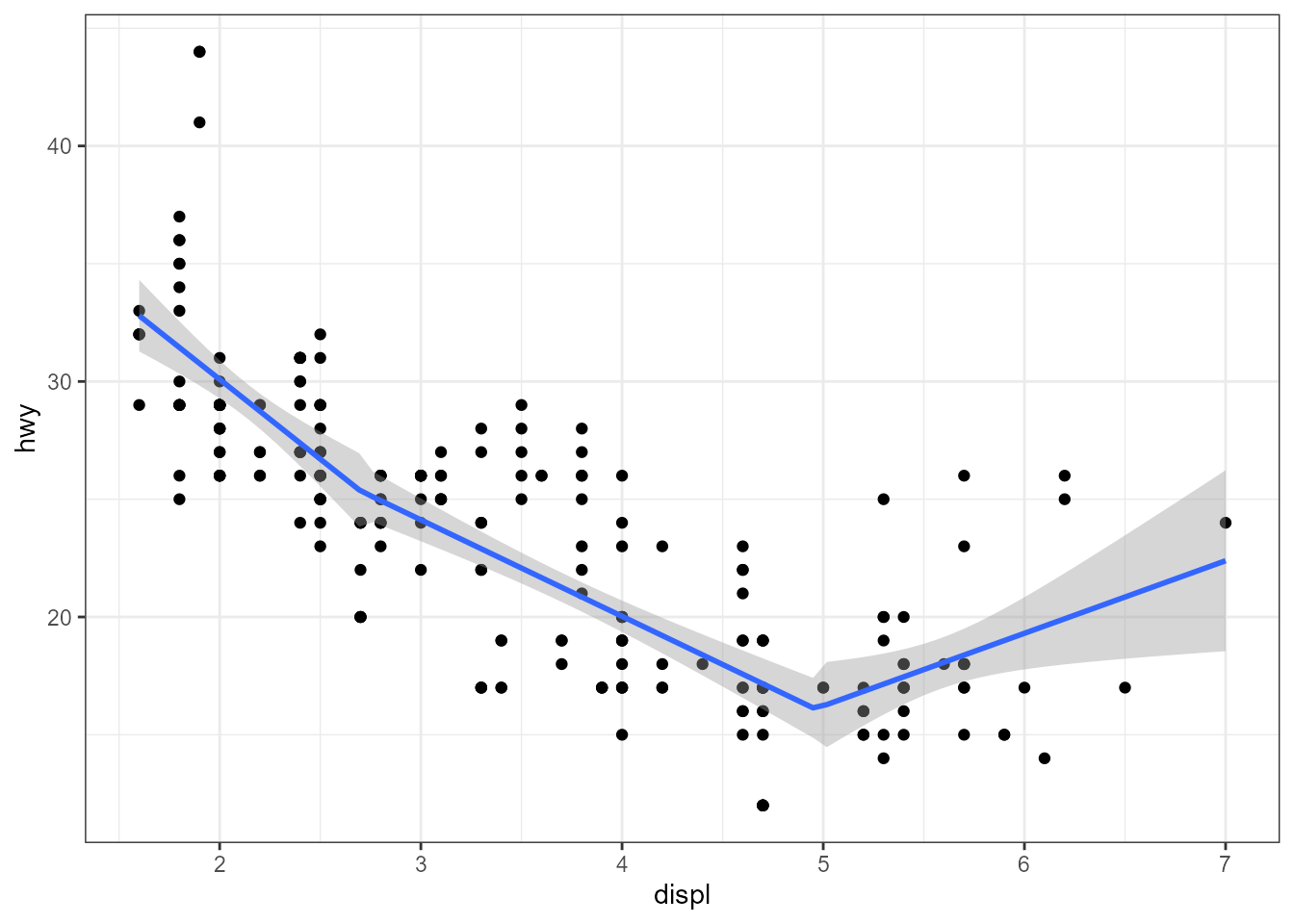
A more complex example with labels, assembled within the call to
aes(). In addition to the intercept and slope for the
leftmost segment, it returns the slope for each segment to the right of
the first one, but not their intercepts. As segment() fits
and returns the position of the knots, which are also returned by
stat_poly_eq() in ‘ggpmisc’ (>= 0.6.3). A label is added
with the knot position, and two regression equations, one for each
segment of the linear spline.
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_eq(aes(label =
paste("italic(x)[cp]~`=`~",
round(after_stat(knots)[[1]][1], 2),
"*\"; L: \"*y~`=`~",
round(after_stat(b_0), 2), #"+",
round(after_stat(b_1), 2), "~x",
"*\"; R: \"*y~`=`~",
round(after_stat(b_0) +
after_stat(knots)[[1]][1] *
(after_stat(b_1) - after_stat(b_2)),
2),
"+",
round(after_stat(b_2), 2), "~x",
sep = "")),
parse = TRUE, output.type = "numeric",
label.x = "right",
formula = y ~ x,
method = lm2segmented.lm) +
stat_poly_eq(use_label("R2", "P", "AIC"),
label.x = "right",
label.y = 0.87,
formula = y ~ x,
method = lm2segmented.lm,
method.args = list(psi = c(3, 5))) +
stat_poly_line(method = lm2segmented.lm,
formula = y ~ x,)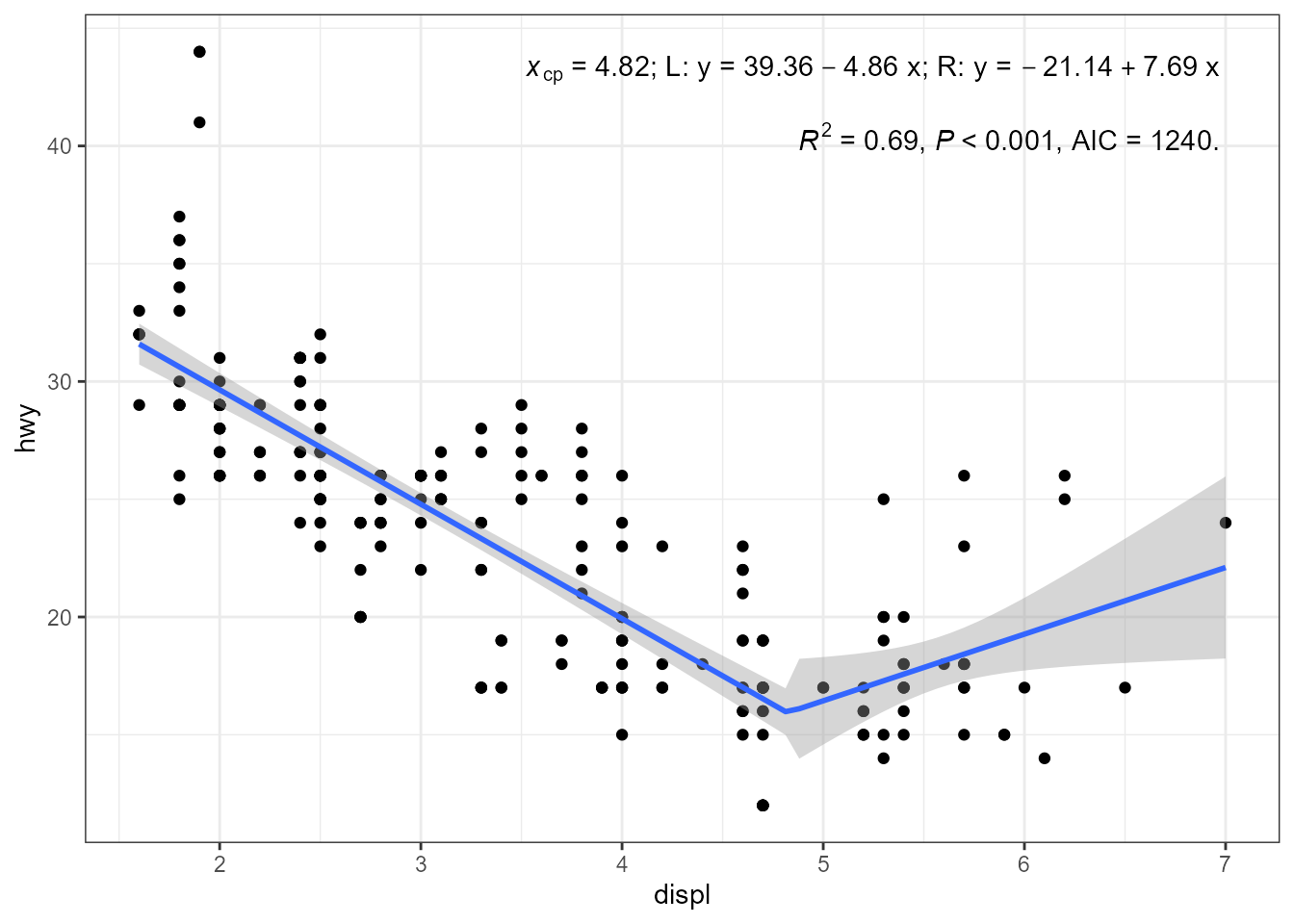
Work-arounds
Some model-fit functions return objects for which no
predict() method exist. In such cases, as users we can
define such a method. More difficult situations can also be faced.
Errors in variables (‘refitME’)
In this section I show a situation I faced when trying to use package
‘refitME’. The functions exported by this package fail when called from
within a function, so they do not currently work if passed as an
argument for method. Below, a temporary work-around based
on a solution provided by the maintainer of ‘refitME’ is shown.
print(citation(package = "refitME", auto = TRUE), bibtex = FALSE)
#> To cite package 'refitME' in publications use:
#>
#> Stoklosa J, Hwang W, Warton D (2025). _refitME: Measurement Error
#> Modelling using MCEM_. doi:10.32614/CRAN.package.refitME
#> <https://doi.org/10.32614/CRAN.package.refitME>, R package version
#> 1.3.1, <https://CRAN.R-project.org/package=refitME>.As ‘refitME’ functions return a model fit object of the same class as
that received as input, a model fitted with lm() could be,
in principle, refit in a user-defined wrapper function as those above,
calling first lm() and re-fitting the obtained model with a
refitME::refitME() as shown in the code chunk below.
However, at the moment the functions in package ‘refitME’ fail when
called from within another function.
lm_EIV <- function(formula, data, ..., sigma.sq.u) {
fm <- lm(formula = formula, data = data, ...)
MCEMfit_glm(mod = fm, family = "gaussian", sigma.sq.u = sigma.sq.u)
}After defining such a function, we could then use our function
lm_EIV() as the method.
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
stat_poly_line(method = "lm_EIV", method.args = c(sigma.sq.u = 0)) +
stat_poly_eq(method = "lm_EIV", method.args = c(sigma.sq.u = 0),
mapping = use_label("eq"),
label.x = "right") +
theme(legend.position = "bottom") +
facet_wrap(~class, ncol = 2)Produces one warning like below for each call of the statistics.
Warning: Computation failed in `stat_poly_eq()`.
Caused by error in `names(new.dat)[c(1, which(names(mod$data) %in% names.w))] <- names(mod$data)[c(1, which(names(mod$data) %in% names.w))]`:
! replacement has length zero```I have reported the problem through a GitHub issue to Jakub Stoklosa, the maintainer of ‘refitME’, and he is looking for a permanent solution. Meanwhile, he has provided a temporary fix that I copy below with a few small edits to the ggplot code. Many thanks to Jakub Stoklosa for his very fast answer!
rm(list = ls(pattern = "*"))
library(refitME)
lm_EIV <- function(formula, data, ..., sigma.sq.u) {
assign("my.data", value = data, envir = globalenv())
fm <- lm(formula = formula, data = my.data, ...)
fit <- refitME(fm, sigma.sq.u)
fit$coefficients <- Re(fit$coefficients)
fit$fitted.values <- Re(fit$fitted.values)
fit$residuals <- Re(fit$residuals)
fit$effects <- Re(fit$effects)
fit$linear.predictors <- Re(fit$linear.predictors)
fit$se <- Re(fit$se)
if ("qr" %in% names(fit)) {
fit$qr$qr <- Re(fit$qr$qr)
fit$qr$qraux <- Re(fit$qr$qraux)
}
class(fit) <- c("lm_EIV", "lm")
return(fit)
}
predict.lm_EIV <- function(object, newdata = NULL, ...) {
preds <- NextMethod("predict", object, newdata = newdata, ...)
if (is.numeric(preds)) {
return(Re(preds))
} else if (is.matrix(preds)) {
return(Re(preds))
} else {
return(preds) # Leave unchanged if not numeric/matrix
}
}Here the limitation of ‘ggplot2’ and ‘ggpmisc’ in that the fit is
recomputed in each layer causes a further difficulty, as with most
algorithms using random numbers, the successive refits do not
necessarily produce the exact same results. In this case, the equation
and line are not matched, and the mismatch can be large for large values
of sigma.sq.u and low replication, especially in the
presence of outliers.
This is something that can most likely be fixed in ‘ggpmisc’ by
setting the seed of the RNG. To check that work-around is working as
expected, we set sigma.sq.u = 0 effectively using an OLS
approach and expecting values nearly identical as with
lm().
ggplot(mpg, aes(x = displ, y = hwy)) +
geom_point() +
stat_poly_line(aes(y = hwy),
method = "lm_EIV",
method.args = list(sigma.sq.u = 0)) +
stat_poly_eq(aes(y = hwy,
label = paste(after_stat(eq.label), after_stat(rr.label),
sep = "~~")),
method = "lm_EIV",
method.args = list(sigma.sq.u = 0),
label.x = "right") +
facet_wrap(~class, ncol = 2)
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
#> [1] 2
We do not know the measurement error for the measurement of
displ, the displacement volume of the engines. For this
example we make up a value: sigma.sq.u = 0.01 expecting
estimates different from above and with lm().
ggplot(mpg, aes(x = displ, y = hwy)) +
geom_point() +
stat_poly_line(aes(y = hwy),
method = "lm_EIV",
method.args = list(sigma.sq.u = 0.01)) +
stat_poly_eq(aes(y = hwy,
label = paste(after_stat(eq.label), after_stat(rr.label),
sep = "~~")),
method = "lm_EIV",
method.args = list(sigma.sq.u = 0.01),
label.x = "right") +
facet_wrap(~class, ncol = 2)
#> [1] 5
#> [1] 11
#> [1] 6
#> [1] 6
#> [1] 6
#> [1] 8
#> [1] 6
#> [1] 5
#> [1] 12
#> [1] 6
#> [1] 6
#> [1] 6
#> [1] 8
#> [1] 6
Transformations and eq.label
In ‘ggplot2’ setting transformations in X and y
scales results in statistics receiving transformed data as input. The
data “seen” by statistics is the same as if the transformation had been
applied within a call to aes(). However, the scales
automatically adjust breaks and tick labels to display the values in the
untransformed scale. When the transformation is applied in the model
formula definition, the transformation is applied later,
but still before the model is fit. all these cases, the model fit is
based on transformed values and thus the estimates refer to them. This
is why, a linear fit remains linear in spite of the transformations.
Only eq.label is affected by transformations in the
sense that the x and y in the default equation refer
to transformed values, rather than those shown in the tick labels of the
axes, i.e., the default model equation label is incorrect. The
correction to apply is to override the x and/or y
symbols in the equation label by an expression that includes the
transformation used. In these examples we fit polynomials by OLS using
lm(), the default method.
ggplot(mpg, aes(x = displ, y = hwy)) +
geom_point() +
stat_poly_line() +
stat_poly_eq(mapping = use_label("eq", "R2", "n", "P"),
eq.with.lhs = "log[10]~hwy~`=`~",
eq.x.rhs = "~displ") +
scale_y_log10() +
expand_limits(y = 50)
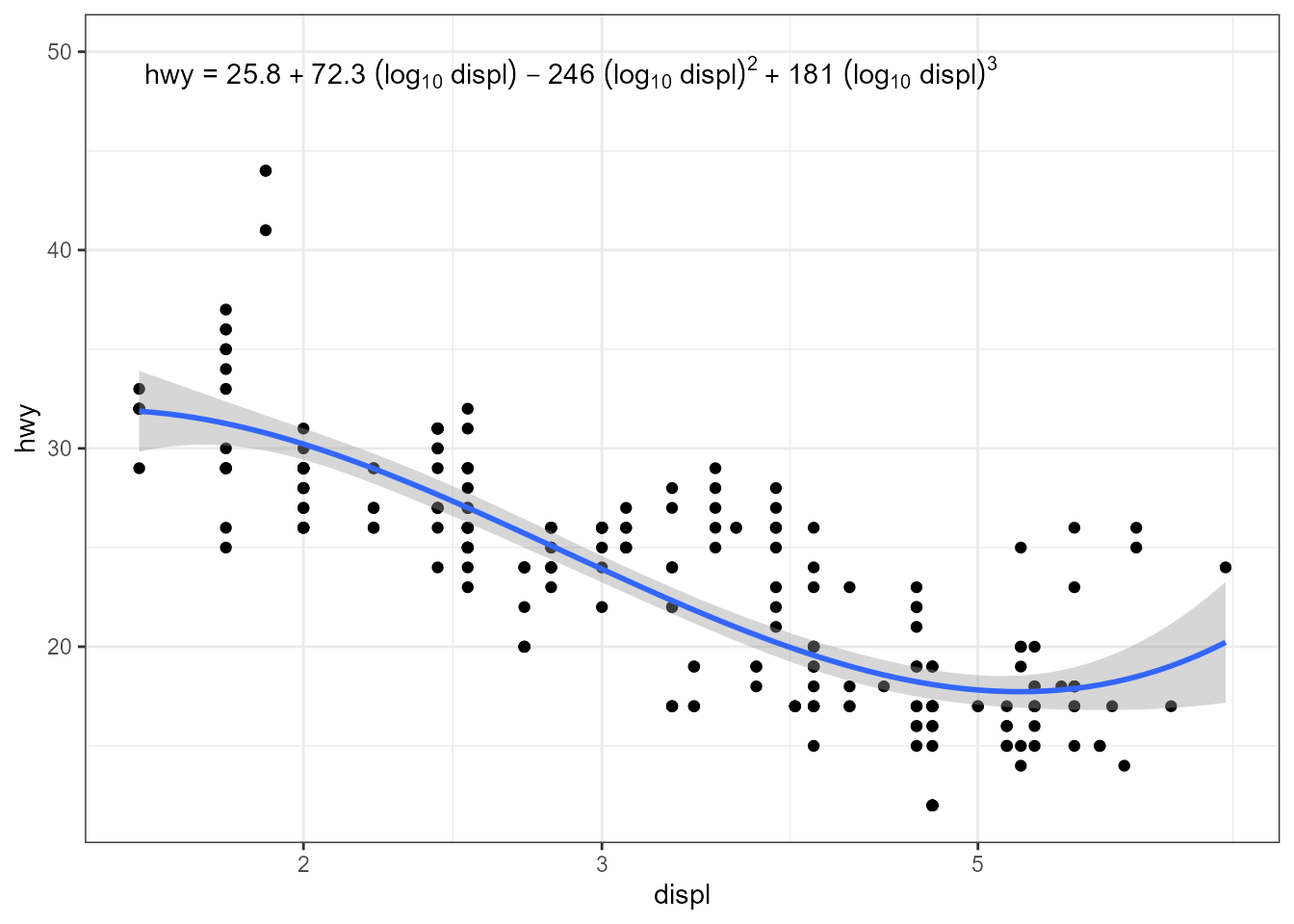
ggplot(mpg, aes(x = displ, y = hwy)) +
geom_point() +
stat_poly_line(formula = y ~ poly(x, 3, raw = TRUE)) +
stat_poly_eq(mapping = use_label("eq"),
formula = y ~ poly(x, 3, raw = TRUE),
eq.with.lhs = "hwy~`=`~",
eq.x.rhs = "~(log[10]~displ)") +
scale_x_log10(name = "displ") +
expand_limits(y = 50)